
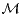 n(
n(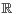 ) et Graphe(A) l’ensemble {(X,AX);X
) et Graphe(A) l’ensemble {(X,AX);X 
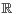 n}.
n}.
a) Montrer que Graphe(A) est un sous-espace vectoriel de 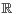 2n et qu’il caractérise A.
2n et qu’il caractérise A.
b) quelle condition un sous-espace vectoriel de 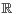 2n est-il le graphe d’une matrice ?
2n est-il le graphe d’une matrice ?
c) Soient (e1 , … , en,f1,…,fn) la base canonique de 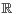 2n et Rotk l’isomorphisme de
2n et Rotk l’isomorphisme de 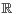 2n qui
échange les composantes selon ek et fk sans toucher aux autres. quelle condition sur A
existe-t-il une matrice Aʹ telle que Graphe(Aʹ) = Rotk(Graphe(A)) ? Dans ce cas, calculer
Aʹ.
2n qui
échange les composantes selon ek et fk sans toucher aux autres. quelle condition sur A
existe-t-il une matrice Aʹ telle que Graphe(Aʹ) = Rotk(Graphe(A)) ? Dans ce cas, calculer
Aʹ.
d) On note Sweepk(A) la matrice Aʹ de la question précédente. Que dire, sous réserve d’existence
à chaque étape, de Sweep1 • Sweep2 • • Sweepn(A) ?
• Sweepn(A) ?
Le corrigé publié dans le numéro précédent était erroné. Nous prions nos lecteurs de bien vouloir accepter nos excuses.
Comme dans l’énoncé, on identifiera Rn avec l’espace des vecteurs colonnes Mn,1(R), dont on notera (E1 , … , En ) la base canonique (qu’on évitera de confondre avec (e1,…,en)).
a) L’ensemble Graphe(A) est l’image de l’application linéaire X (X,AX). C’est donc un
sous-espace vectoriel de R2n. L’application induite, de Rn dans Graphe(A), est une bijection et il
existe, pour tout k, un unique vecteur Ck
(X,AX). C’est donc un
sous-espace vectoriel de R2n. L’application induite, de Rn dans Graphe(A), est une bijection et il
existe, pour tout k, un unique vecteur Ck  Rn, tel que (Ek,Ck)
Rn, tel que (Ek,Ck)  Graphe(A). Ce
vecteur n’étant autre que la k-ième colonne, on voit que le graphe caractérise la matrice
A.
Graphe(A). Ce
vecteur n’étant autre que la k-ième colonne, on voit que le graphe caractérise la matrice
A.
b) Soit G un sous-espace vectoriel de R2n. Ce qui précède montre que si G est le graphe d’une
matrice, alors la première projection (X,Y )  Rn × Rn
Rn × Rn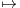 X induit un isomorphisme de G dans
Rn. Cette condition est aussi suffisante car, si elle est vérifiée, G est le graphe de la matrice
(C1 , … , Cn ) où Ck est l’unique vecteur tel que (Ek,Ck)
X induit un isomorphisme de G dans
Rn. Cette condition est aussi suffisante car, si elle est vérifiée, G est le graphe de la matrice
(C1 , … , Cn ) où Ck est l’unique vecteur tel que (Ek,Ck)  G.
G.
c) On a Graphe (A) = V ect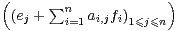 . Donc Rotk(Graphe(A)) est engendré par
le vecteur ak,k ek + fk +
. Donc Rotk(Graphe(A)) est engendré par
le vecteur ak,k ek + fk + 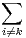 ai,kfi et les vecteurs ej + ak,jek +
ai,kfi et les vecteurs ej + ak,jek + 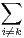 ai,jfi pour j ⁄= k. D’après b) ,
c’est le graphe d’une matrice Aʹ si et seulement si ak,kEk et (Ej + ak,jEk)j⁄=k forment une
base de R n , soit ak,k ⁄= 0. En notant Cʹi les colonnes de Aʹ et Ci les colonnes de A, il
vient :
ai,jfi pour j ⁄= k. D’après b) ,
c’est le graphe d’une matrice Aʹ si et seulement si ak,kEk et (Ej + ak,jEk)j⁄=k forment une
base de R n , soit ak,k ⁄= 0. En notant Cʹi les colonnes de Aʹ et Ci les colonnes de A, il
vient :
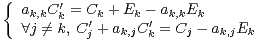
d’où
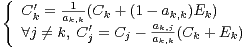
d) Posons B = Sweep1 • Sweep2 • • Sweepn(A). On a
• Sweepn(A). On a
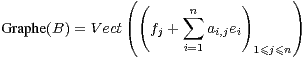
soit, en notant Cʹj la j-ieme colonne de B : ∀j, 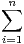 ai,jCʹj = Ej, ou encore AB = In.
Ainsi
ai,jCʹj = Ej, ou encore AB = In.
Ainsi
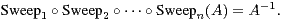
Remarque : On obtient ainsi un algorithme de calcul de A-1 parent proche de l’algorithme de
Gauss (mais non identique).
[Liste des corrigés]

