[Épreuves orales des concours]
a) Soit d la distance maximale entre deux sommets de G. Montrer que la maille, si elle existe, est majorée par 2d + 1.
b) Montrer qu’un graphe est biparti (c’est-à-dire tel que l’ensemble des sommets se partitionne en deux parties non vides S1 et S2 telles que toute arête joigne un sommet de S1 et un sommet de S2) si et seulement s’il ne contient pas de cycle de longueur impaire. Qu’en déduire sur la maille d’un tel graphe ?
c) Montrer qu’un graphe à n sommets qui contient au plus un cycle, contient au plus n arêtes.
d) Montrer que la maille d’un graphe à n sommets et au moins n + 1 arêtes est majorée par
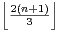 .
.
e) Soit G un graphe tel que le plus petit degré δ d’un sommet et la maille m soient supérieurs
ou égaux à 3. Montrer que, si m est pair, le nombre de sommets est alors minoré par
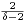 ((δ - 1)m⁄2 - 1).
((δ - 1)m⁄2 - 1).
 Σω et tout automate déterministe fini
Σω et tout automate déterministe fini  = (Q,q0,F,δ), on associe la suite
ρ
= (Q,q0,F,δ), on associe la suite
ρ (m) = (qk )k
(m) = (qk )k N
N  QN vérifiant, pour tout k
QN vérifiant, pour tout k  N, qk+1 = δ(qk,mk).
N, qk+1 = δ(qk,mk).
Un langage L ⊂ Σω de mots infinis est
∙ ∃-reconnaissable s’il existe un automate 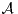 tel que
tel que
L = {m  Σω , ρ
Σω , ρ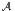 (m) contient au moins un état acceptant} ;
(m) contient au moins un état acceptant} ;
∙ ∀-reconnaissable s’il existe un automate 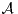 tel que
tel que
L = {m  Σω , ρ
Σω , ρ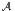 (m) ne contient que des états acceptants} ;
(m) ne contient que des états acceptants} ;
∙ ω-reconnaissable s’il existe un automate 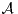 tel que
tel que
L = {m  Σω , ρ
Σω , ρ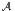 (m) contient un nombre infini d’états acceptants} ;
(m) contient un nombre infini d’états acceptants} ;
∙ ω -reconnaissable s’il existe un automate 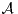 tel que
tel que
L = {m  Σω , ρ
Σω , ρ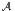 (m) contient un nombre fini d’états acceptants}.
(m) contient un nombre fini d’états acceptants}.
a) Montrer que le langage des mots (infinis) contenant au moins deux b est ∃-reconnaissable.
b) Montrer que le langage des mots (infinis) contenant une infinité de b est ω-reconnaissable.
c) Montrer que tout langage ∃-reconnaissable est ω-reconnaissable puis que la réciproque est fausse.
d) Montrer que le langage des mots (infinis) ne contenant pas le facteur bb mais contenant au moins une fois le facteur bab est ω-reconnaissable mais pas ∀-reconnaissable.
e) Exhiber un langage ω-reconnaissable qui n’est pas ω-reconnaissable puis un langage ω-reconnaissable qui n’est pas ω-reconnaissable.
On admet le théorème suivant
Théorème 1.Soit L un langage rationnel. Alors il existe un unique (à isomorphisme près)
automate déterministe complet 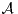 reconnaissant L et tel que tout automate déterministe
complet
reconnaissant L et tel que tout automate déterministe
complet 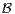 reconnaissant L admet plus d’états que
reconnaissant L admet plus d’états que 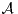 .
.
On note ind (L) le nombre d’états de 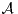 , noté |
, noté |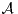 |.
|.
b) Déterminer tous les langages rationnels L sur l’alphabet Σ = {a} tels que ind(L) ≤ 2.
Un langage rationnel L est composé s’il existe des automates complets 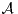 1, …,
1, …, 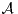 k tels que, pour
tout i, |
k tels que, pour
tout i, |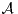 i | < ind (L) et L = ⋂
i | < ind (L) et L = ⋂
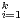 L(
L(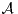 i). Un langage rationnel non composé est dit
premier.
i). Un langage rationnel non composé est dit
premier.
c) Déterminer si les langages suivants sont composés ou premiers :
i) L1 = {a, b}* sur l’alphabet Σ = {a,b} ii) L2 = {a} sur l’alphabet Σ = {a}
iii) L3 = {a,b} sur l’alphabet Σ = {a,b}
d) Soit k > 0 un entier qui n’est pas la puissance d’un nombre premier. Montrer que le langage (ak )* est composé sur l’alphabet Σ = {a}.
e) Déterminer un algorithme qui, à partir d’un automate 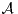 tel que L = L(
tel que L = L(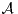 ) et ind(L) = |
) et ind(L) = |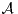 |,
détermine si le langage L est composé ou premier.
|,
détermine si le langage L est composé ou premier.
f) Montrer le théorème admis.
On note γ(G) le cardinal du plus petit ensemble dominant de G.
a) Calculer γ(Pn), où Pn désigne le chemin à n sommets.
b) Montrer que γ(G) ≤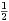 |S|, et exhiber un cas d’égalité.
|S|, et exhiber un cas d’égalité.
c) Exhiber une infinité de graphes vérifiant γ(G) ≥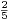 |S|.
|S|.
Un graphe est une griffe s’il est de la forme du graphe biparti complet K1,3.
d) Montrer que si aucun des sous-graphes induits de G n’est une griffe, alors il existe un ensemble dominant minimal X tel que le graphe induit G[X] est sans arête.
e) Trouver un algorithme calculant γ(G) lorsque G est un arbre.
 Sn.
Sn.
a) Soient x1 , …, xp des entiers tels que, pour tout k, 0 ≤ xk ≤ k. La suite finie (x1,…,xp) s’appelle
l’écriture factorielle de l’entier n = 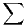
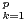 xkk!. Montrer que cette écriture existe et est unique
pour tout entier naturel n.
xkk!. Montrer que cette écriture existe et est unique
pour tout entier naturel n.
b) On représente une permutation σ  Sn par le mot σ(1)…σ(n). On appelle ordre de σ le
nombre de permutations de Sn dont la représentation est strictement inférieure au mot
représentant σ pour l’ordre lexicographique. Donner un algorithme calculant l’ordre de
σ.
Sn par le mot σ(1)…σ(n). On appelle ordre de σ le
nombre de permutations de Sn dont la représentation est strictement inférieure au mot
représentant σ pour l’ordre lexicographique. Donner un algorithme calculant l’ordre de
σ.
c) Donner un algorithme calculant la permutation suivant σ selon l’ordre lexicographique de leurs représentations.
d) Pour tout σ  Sn , notons Xi(σ) la longueur du cycle de σ contenant l’entier i. Montrer en
utilisant une représentation appropriée de σ que :
Sn , notons Xi(σ) la longueur du cycle de σ contenant l’entier i. Montrer en
utilisant une représentation appropriée de σ que :
∀k  {1, … , n}, |{σ
{1, … , n}, |{σ  Sn, X1(σ) = k}| = (n - 1)!.
Sn, X1(σ) = k}| = (n - 1)!.
e) Donner un algorithme donnant avec une probabilité uniforme une permutation σ telle que X1 (σ) = k.
Un langage monitorable est un sous-ensemble de l’ensemble L des mots infinis Σω tel qu’il existe
un moniteur tel que pour tout mot fini u  Σ* :
Σ* :
– si δ* (q0 , u) = ⊤ alors uΣω ⊆ L ; – si δ*(q0,u) = ⊥ alors uΣω ∩ L = ∅.
a) Interpréter la notion de langage monitorable.
b) Déterminer si les langages suivants sur l’alphabet Σ = {a,b,c} sont monitorables et si oui, donner un moniteur avec un maximum d’états accessibles possibles
i) L1 , l’ensemble des mots contenant une infinité de a,
ii) L2 , l’ensemble des mots contenant au moins un b,
iii) L3 , l’ensemble des mots contenant au moins un b mais ne contenant pas de c.
c) Soit L ⊆ Σω . Soit u  Σ* tel qu’il existe un mot v
Σ* tel qu’il existe un mot v  Σ* vérifiant uvΣω ⊆ L. Montrer que L est
monitorable. Reprendre la question avec l’hypothèse uvΣω ∪ L = ∅.
Σ* vérifiant uvΣω ⊆ L. Montrer que L est
monitorable. Reprendre la question avec l’hypothèse uvΣω ∪ L = ∅.
Considérons le théorème suivant :
Théorème 2.Un langage L est monitorable si, et seulement si, il existe un entier n  N et
un mot v
N et
un mot v  Σ* vérifiant |v|≤ (n + 1)2 tel que ∀u
Σ* vérifiant |v|≤ (n + 1)2 tel que ∀u  Σ*, uvΣω ⊆ L ou uvΣω ∪ L = ∅.
Σ*, uvΣω ⊆ L ou uvΣω ∪ L = ∅.
d) Donner une interprétation de ce théorème.
e) Prouver le théorème.
a) Déterminer Attr1(F) dans la configuration suivante.
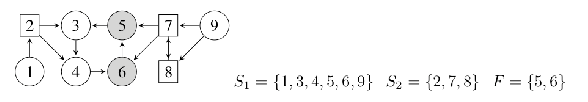
b) Déterminer un algorithme de complexité O(|S| + |A|) permettant de calculer Attr1(F) lorsque G est acyclique.
c) Montrer que le jeu des allumettes, où les deux joueurs piochent alternativement 1, 2 ou 3 allumettes dans un paquet jusqu’à épuisement (on considère que celui ramassant la dernière gagne), peut-être modélisé comme un jeu de la forme précédente.
d) tendre l’algorithme de la question b) au cas général.
On considère maintenant le jeu infini où J1 gagne s’il arrive à faire passer le jeton une infinité de fois par un sommet de F .
e) Montrer que s  S est gagnant pour J1 si et seulement si J1 possède une stratégie faisant
passer le jeton au moins |S| fois par F depuis s.
S est gagnant pour J1 si et seulement si J1 possède une stratégie faisant
passer le jeton au moins |S| fois par F depuis s.
f) En déduire une algorithme de complexité O(|S||A|) calculant les positions gagnantes pour J1 .
g) Montrer que les sommets de Attr2(Attr1(F)) sont gagnants pour J2.
h) En déduire un nouvel algorithme de même complexité que le précédent.
 S
et
S
et
- (S, +) est un monoïde commutatif de neutre 0
- (S, ⊗) est un monoïde commutatif de neutre 1
- ⊗ est distributive sur +.
a) Parmi les quintuplets suivants, lesquels sont des semi-anneaux : i) (N,+,⋅,0,1),
ii) (N , min , ⋅, 0, 1), iii) (N,max,⋅,0,1), iv) (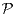 (X),∪,∩, ∅,X), si X est un ensemble ?
(X),∪,∩, ∅,X), si X est un ensemble ?
Soit Q un ensemble de sommets, I, F ⊂ Q (sommets initiaux, finaux). On dit que G = (Q,γ,I,F)
est un graphe orienté sur le semi-anneau (S,+,⊗,0,1) lorsque γ associe à chaque couple
(p, q)  Q × Q un élément de S, appelé coût. On désigne par chemin un chemin dans un graphe au
sens usuel. On étend la définition de coût aux chemins. Si c = x0…xn est un chemin, alors
γ(c) =
Q × Q un élément de S, appelé coût. On désigne par chemin un chemin dans un graphe au
sens usuel. On étend la définition de coût aux chemins. Si c = x0…xn est un chemin, alors
γ(c) = 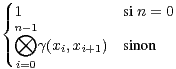
Dans la suite de cette question, on considère un graphe orienté sur le semi-anneau (N,+,⋅,0,1),
d’ensemble de sommets {1,…,n}.
Pour tout (p, q)  Q2 et r
Q2 et r  {0,…,n}, on définit γ
{0,…,n}, on définit γ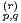 par :
par :
γ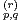 =
= 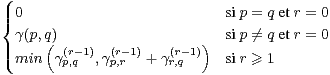
b) Que représente γ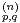 ?
?
c) Soit Σ un alphabet fini. Donner +, ⊗, 0 et 1 pour que (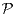 (Σ*),+,⊗,0,1) soit un
semi-anneau.
(Σ*),+,⊗,0,1) soit un
semi-anneau.
d) Utiliser la technique de la deuxième question pour définir le langage 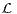 (A) reconnu par un
automate fini non déterministe A.
(A) reconnu par un
automate fini non déterministe A.
e) Définir de même l’expression régulière associée à un tel automate.
Soit G = (Q, γ, I,F) un graphe orienté et n  N. On définit Π(n) comme l’ensemble de tous les
chemins de longueur n d’un sommet de I à un sommet de F . On définit de plus π(n) par
π(n) =
N. On définit Π(n) comme l’ensemble de tous les
chemins de longueur n d’un sommet de I à un sommet de F . On définit de plus π(n) par
π(n) = 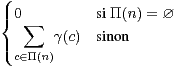
f) Donner un algorithme efficace de calcul de π(n).
AX ≤ B, d’inconnue X = t(x1,…,xn)  Rn, où A
Rn, où A 
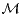 m,n(R) et B
m,n(R) et B  Rm.
Rm.
a) i) Montrer que si le système (S) contient deux inéquations (I1) et (I2) avec des coefficients en x1 respectivement > 0 et < 0, on peut trouver une inéquation (I0) ne mettant pas en jeu la variable x1 et équisatisfiable à la conjonction (I1) ∧ (I2).
ii) En déduire un algorithme de résolution d’un tel système d’inéquations linéaires.
iii) Quelle est sa complexité dans le pire des cas ?
b) On cherche à améliorer l’algorithme précédent. chaque étape de son exécution permettant de supprimer une inconnue xi, on générait une nouvelle liste d’inéquations. On va maintenant de plus associer à chaque nouvelle inéquation son historique : la partie de {1,…,n} contenant les indices des inéquations du système (S) de départ dont l’inéquation est combinaison linéaire.
i) Expliquer comment on calcule les historiques.
ii) Montrer qu’on peut, à chaque étape de l’algorithme, ne garder que les nouvelles inéquations d’historique minimal (au sens de l’inclusion).
iii) En déduire une amélioration de l’algorithme précédent. Estimer sa complexité.
[Épreuves orales des concours]

