[Épreuves orales des concours]Algèbre
Calculer S + T et ST . En déduire S et T .
 N *. Calculer
N *. Calculer 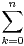 e2ik. En déduire la valeur de
e2ik. En déduire la valeur de 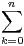 cos(2k).
cos(2k).
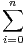
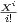 et Qn(X) = P
et Qn(X) = P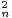 (X) -Pn(2X). Montrer que 0
est racine de Qn de multiplicité (n + 1).
(X) -Pn(2X). Montrer que 0
est racine de Qn de multiplicité (n + 1).
 C; P(z) = 0
C; P(z) = 0 1 ≤|z|≤ 2.
1 ≤|z|≤ 2.
b) Soit P = a0 + a1X +  + anXn
+ anXn  R[X] avec a0 ≥ a1 ≥
R[X] avec a0 ≥ a1 ≥ ≥ an > 0. On pose
Q = (1 - X)P. Soit z
≥ an > 0. On pose
Q = (1 - X)P. Soit z  C tel que Q(z) = 0. Montrer que a0 =
C tel que Q(z) = 0. Montrer que a0 = 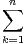 (ak-1 -ak)zk + anzn+1. En
déduire que si P(z) = 0 alors |z|≥ 1.
(ak-1 -ak)zk + anzn+1. En
déduire que si P(z) = 0 alors |z|≥ 1.
c) Soit P = a0 + a1X +  + anXn
+ anXn  R[X] où les ai sont dans R+*. On pose
r = min
R[X] où les ai sont dans R+*. On pose
r = min 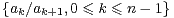 . Montrer que les racines de P sont de module
≥ r.
. Montrer que les racines de P sont de module
≥ r.
Ind. Considérer  = P(rX).
= P(rX).

 3(R) telle que A2 = 0 et A≠0. Montrer que A est semblable à
3(R) telle que A2 = 0 et A≠0. Montrer que A est semblable à  .
.
a) Les sous-espaces P et D sont-ils supplémentaires dans E ?
b) Déterminer la matrice dans la base canonique du projecteur sur P parallèlement à D.

 (E) de rang 1 et a
(E) de rang 1 et a  E tels que
Kerf ⊕ Vect (a) = E.
E tels que
Kerf ⊕ Vect (a) = E.
a) Montrer que Imf = Vect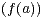 .
.
b) Montrer qu’il existe λ  R tel que f2 = λf. Déterminer les valeurs propres de f en fonction de
λ.
R tel que f2 = λf. Déterminer les valeurs propres de f en fonction de
λ.
c) Soit H un sous-espace de E tel que E = H ⊕ Vect(a). Soit u 
 (E) tel que : ∀x
(E) tel que : ∀x  H,
u(x) = x.
H,
u(x) = x.
i) Montrer qu’il existe μ  R tel que u(a) - μa
R tel que u(a) - μa  H. En déduire que Im
H. En déduire que Im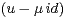 ⊂ H.
⊂ H.
ii) Montrer que u2 - (μ + 1)u + μid = 0. Si μ = 1, l’endomorphisme u est-il diagonalisable ?
a) Montrer que Im(f) et Ker(g) sont supplémentaires dans E.
b) Justifier que f(Im(g)) = Im(f).
 R* et u
R* et u 
 (E) tel que u2 = -k2 id.
(E) tel que u2 = -k2 id.
a) Montrer que u ne possède pas de valeur propre réelle.
b) Soit a  E \ {0}. Montrer que (a,u(a)) est libre.
E \ {0}. Montrer que (a,u(a)) est libre.
c) Soient a, b dans E avec b ⁄ Vect(a,u(a)). Montrer que
Vect(a,u(a)). Montrer que 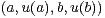 est une base de E.
Quelle est la matrice de u dans cette base ?
est une base de E.
Quelle est la matrice de u dans cette base ?
 ou
C.
ou
C.
a) On suppose que u et v commutent. Montrer que Ker(u) et Im(u) sont stables par v.
a) Montrer que u laisse stable toutes les droites de E si et seulement si u est une homothétie.
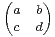

 2 (C) et M
2 (C) et M 
 n(C).
n(C).
a) Montrer que P =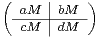 s’écrit comme le produit de deux matrices, la seconde étant diagonale par blocs.
s’écrit comme le produit de deux matrices, la seconde étant diagonale par blocs.
b) En déduire det(P).

 n (
n ( )
)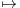 MD - DM.
MD - DM.
a) Montrer que μ est un endomorphisme de  n(
n( ).
).
b) Trouver Ker μ.
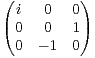 .
.
a) i) Calculer M2. La matrice M est-elle inversible ?
ii) Exprimer, pour n  N*, Mn en fonction de M et M2.
N*, Mn en fonction de M et M2.
b) Soit M 
 3 (R) telle que M3 + M = 0 et f l’endomorphisme canoniquement associé à M.
On suppose que f est injectif.
3 (R) telle que M3 + M = 0 et f l’endomorphisme canoniquement associé à M.
On suppose que f est injectif.
i) Montrer que M est inversible et que M2 = -I3.
ii) Calculer det(M2) et montrer qu’on aboutit à une absurdité.
 -espace vectoriel, f
-espace vectoriel, f 
 (E) et C(f) = {g
(E) et C(f) = {g 
 (E),f • g = g • f}.
(E),f • g = g • f}.
a) Montrer que C(f) est un  -espace vectoriel
-espace vectoriel
b) Soit (e1 , e2 ) la base canonique de  2. Soit x = x1e1 + x2e2
2. Soit x = x1e1 + x2e2  R2. Donner une condition
nécessaire et suffisante pour que (e1 - x,e2 - x) soit une base de
R2. Donner une condition
nécessaire et suffisante pour que (e1 - x,e2 - x) soit une base de  2.
2.
c) Généralisation. Soit (e1,…,en) la base canonique de  n et soit x = x1e1 +
n et soit x = x1e1 +  + xnen dans
+ xnen dans
 n .
n .
i) Donner une condition nécessaire et suffisante pour que (e1 - x,…,en - x) soit une base de
 n .
n .
ii) Soit f l’endomorphisme de  n tel que pour tout entier i
n tel que pour tout entier i  [[1,n]], f(ei) = ei - x. Trouver
les valeurs propres de f avec leurs multiplicités.
[[1,n]], f(ei) = ei - x. Trouver
les valeurs propres de f avec leurs multiplicités.
iii) Sous quelles conditions l’endomorphisme f est-il diagonalisable ?
iv) Déterminer la dimension du commutant de f.
 .
.
 .
.
 R4, soit A(a,b,c,d) =
R4, soit A(a,b,c,d) = .
.
a) Déterminer le polynôme caractéristique de A(a,b,c,d).
b) Soit x 
 . La matrice A(x,-x2,x3,0) est-elle diagonalisable sur
. La matrice A(x,-x2,x3,0) est-elle diagonalisable sur  ? sur C ?
? sur C ?
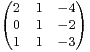 ,
B =
,
B =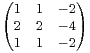 .
.
a) Calculer A2 , A3. En déduire une expression de An pour tout n  N.
N.
b) Calculer les valeurs propres de A. Est-elle diagonalisable ?
c) Montrer que les vecteurs propres de A sont aussi des vecteurs propres de B. La matrice B est-elle diagonalisable ?
d) Soient (x, y) 
 2 et M(x,y) = xA + yB. Montrer que M(x,y) est diagonalisable et donner
l’expression de (M(x,y))n pour tout n
2 et M(x,y) = xA + yB. Montrer que M(x,y) est diagonalisable et donner
l’expression de (M(x,y))n pour tout n  N.
N.
 R
R xsin(x), b : x
xsin(x), b : x  R
R xcos(x) et E = V ect(sin,cos,a,b). Pour
toute fonction f
xcos(x) et E = V ect(sin,cos,a,b). Pour
toute fonction f  E, on pose D(f) = fʹ.
E, on pose D(f) = fʹ.
a) Montrer que D appartient à  (E).
(E).
b) Quelle est la matrice de D dans la base (sin,cos,a,b) ?
c) Déterminer les valeurs propres de D et calculer D-1.
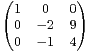 .
.
a) Déterminer les valeurs propres (complexes) de A. La matrice A est-elle diagonalisable ?
b) Calculer P(A). En déduire A-1.
c) Montrer que A est semblable à T = .
.
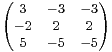 et B =
et B = sont semblables.
sont semblables.
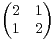 et B =
et B =  . La matrice B est-elle
diagonalisable ? Trouver son rang, ses valeurs propres ; préciser les multiplicités des valeurs
propres.
. La matrice B est-elle
diagonalisable ? Trouver son rang, ses valeurs propres ; préciser les multiplicités des valeurs
propres.

 n(
n( ), P =
), P =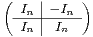 et B =
et B = .
.
a) Montrer que P est inversible et trouver son inverse.
b) Montrer que B est diagonalisable si et seulement si A l’est.

 2 et M =
2 et M =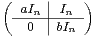 .
Trouver une condition nécessaire et suffisante sur a et b pour que M soit diagonalisable.
.
Trouver une condition nécessaire et suffisante sur a et b pour que M soit diagonalisable.

 n(
n( )
)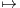 M + tM.
M + tM.
a) Montrer que f est un endomorphisme de  n(
n( ).
).
b) Est-il diagonalisable ?
 n(
n( ) d’expression Φ(M) = M - tr(M)In.
) d’expression Φ(M) = M - tr(M)In.
a) Déterminer les éléments propres de Φ. L’endomorphisme Φ est-il diagonalisable ?
b) Déterminer sa trace, son déterminant et son polynôme caractéristique.
 n[X] et f : P
n[X] et f : P  E
E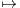
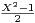 Pʹʹ- XPʹ + P .
Pʹʹ- XPʹ + P .
a) Montrer que f est un endomorphisme de E.
b) On suppose que n = 3.
i) Donner la matrice de f dans la base canonique de E.
ii) Montrer que f est un projecteur ; déterminer Ker(f) et Im(f).
c) On suppose maintenant que n ≥ 4.
i) Montrer que dim(Ker(f)) ≤ 2, et en déduire que Ker(f) = V ect(X,1 + X2).
ii) Montrer que (f(1),f(X3),f(X4),…,f(Xn)) est une base de Im(f).
iv) Montrer que si Q  Imf alors Qʹ(1) = Qʹ(-1) = 0.
Imf alors Qʹ(1) = Qʹ(-1) = 0.
En déduire que Im(f) = {Q  E, Qʹ(1) = Qʹ(-1) = 0}.
E, Qʹ(1) = Qʹ(-1) = 0}.
v) Calculer les valeurs propres de f. Cet endomorphisme est-il diagonalisable ?
 Rn[X]
Rn[X] Pʹʹ- 2XPʹ.
Pʹʹ- 2XPʹ.
a) Justifier que f est un endomorphisme de Rn[X].
b) Soit k  {0, … ,n}. Montrer qu’il existe un unique polynôme Pk unitaire de degré k tel que
f(Pk ) = -2kPk .
{0, … ,n}. Montrer qu’il existe un unique polynôme Pk unitaire de degré k tel que
f(Pk ) = -2kPk .
a) On suppose A inversible. Montrer que χAB = χBA.
b) On suppose A non inversible. Montrer que A-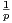 In est inversible pour p
In est inversible pour p  N* assez grand. En
déduire que χAB = χBA.
N* assez grand. En
déduire que χAB = χBA.
 3 de sa structure euclidienne canonique.
3 de sa structure euclidienne canonique.
a) Soit H le sous-espace vectoriel de  3 d’équation x - y + z = 0. Déterminer le projeté
orthogonal de X
3 d’équation x - y + z = 0. Déterminer le projeté
orthogonal de X  R3 sur l’orthogonal de H.
R3 sur l’orthogonal de H.
b) En déduire le projeté orthogonal de X sur H, puis la matrice dans la base canonique de la projection orthogonale sur H.
c) Déterminer la matrice dans la base canonique de la symétrie orthogonale par rapport à H.
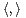 l’application définie sur R[X] × R[X] par
l’application définie sur R[X] × R[X] par 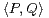 =
= 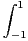
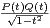 d t.
d t.
a) Montrer l’existence de 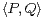 pour tous P,Q
pour tous P,Q  R[X]. Montrer que
R[X]. Montrer que 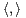 est un produit scalaire
sur R [X].
est un produit scalaire
sur R [X].
b) Soit n  N . Montrer l’existence et l’unicité d’un polynôme Tn tel que, pour tout θ
N . Montrer l’existence et l’unicité d’un polynôme Tn tel que, pour tout θ  R,
Tn (cos θ) = cos (nθ).
R,
Tn (cos θ) = cos (nθ).
c) Montrer que la famille (Tn)n N est une famille orthogonale.
N est une famille orthogonale.
d) Soit F = R 1 [X]. Calculer la distance de X2 à F .
 ]0,π[ et v = (v1,v2) avec v1 = ε1 et v2 = (cosθ)ε1 + (sinθ)ε2. Soit
φ
]0,π[ et v = (v1,v2) avec v1 = ε1 et v2 = (cosθ)ε1 + (sinθ)ε2. Soit
φ 
 (R 2 ) dont la matrice dans v est M =
(R 2 ) dont la matrice dans v est M =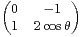 .
.
a) Calculer ∥v1 ∥2, ∥v2∥2 et ⟨v1,v2⟩.
b) Soit y = y1 v1 + y2v2 dans  2. Calculer ∥y∥2 et ∥φ(y)∥2. Montrer que φ appartient à
2. Calculer ∥y∥2 et ∥φ(y)∥2. Montrer que φ appartient à
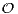 (
( 2 ).
2 ).
c) Soit P la matrice de passage de ε à v. Calculer P-1.
d) Exprimer la matrice Mʹ de φ dans la base canonique.

 (E) tel que ∀x
(E) tel que ∀x  E, ⟨f(x),x⟩ = 0.
E, ⟨f(x),x⟩ = 0.
a) Montrer que ∀(x,y)  E2, ⟨f(y),x⟩ = -⟨f(x),y⟩.
E2, ⟨f(y),x⟩ = -⟨f(x),y⟩.
b) Comparer Ker(f) et l’orthogonal de Im(f).
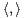 ) un espace euclidien, r et p deux projecteurs orthogonaux de E. Soit λ
une valeur propre non nulle de p • r associée au vecteur propre u.
) un espace euclidien, r et p deux projecteurs orthogonaux de E. Soit λ
une valeur propre non nulle de p • r associée au vecteur propre u.
a) Montrer que u est dans Imp et que r(u) - λu est dans (Imp)⊥.
b) Montrer que λ∥u∥2 = ∥r(u)∥2.
c) Montrer que λ est dans [0,1].
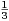
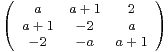 . Préciser les valeurs de a pour lesquelles cette matrice est orthogonale. Déterminer alors les valeurs
propres.
. Préciser les valeurs de a pour lesquelles cette matrice est orthogonale. Déterminer alors les valeurs
propres.
 (
( +*)3 et M =
+*)3 et M = 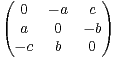 .
.
a) Montrer que M + I3 est inversible.
b) Soit K = (M - I3)(M + I3)-1. Montrer que K est une matrice orthogonale.
 n(
n( ), et on considère les
matrices M = In + A et N = In - A. Soit X appartenant à
), et on considère les
matrices M = In + A et N = In - A. Soit X appartenant à  n,1(
n,1( ).
).
a) Calculer t (t XAX) et en déduire que tXAX = 0.
b) Montrer que si A possède une valeur propre réelle alors celle-ci est égale à 0. En déduire que N et M sont inversibles.
c) Montrer que M et N commutent, que M et N-1 commutent. On pose W = MN-1. Montrer que W est une matrice orthogonale et que - 1 n’est pas valeur propre de W .
d) Soit U 
 n (
n ( ) dont - 1 n’est pas valeur propre. Montrer qu’il existe une unique matrice
antisymétrique A
) dont - 1 n’est pas valeur propre. Montrer qu’il existe une unique matrice
antisymétrique A 
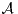 n(
n( ) telle que U = (In - A)(In + A)-1.
) telle que U = (In - A)(In + A)-1.
 N* et M
N* et M 
 n(R) telle que
n(R) telle que 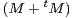 p = 0. Montrer que M est
antisymétrique.
p = 0. Montrer que M est
antisymétrique.
b) Trouver M 
 2(C) telle que
2(C) telle que 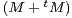 2 = 0 et (M + tM)≠0.
2 = 0 et (M + tM)≠0.
 Im(f). Montrer que y est dans l’orthogonal de Ker(f). En déduire que
(Im (f))⊥ = Ker(f).
Im(f). Montrer que y est dans l’orthogonal de Ker(f). En déduire que
(Im (f))⊥ = Ker(f).

 n(C), on pose ∥A∥ = max
n(C), on pose ∥A∥ = max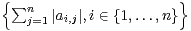 et
ρ(A) = max
et
ρ(A) = max 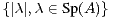 .
.
a) Soit Aθ =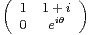 . Calculer ∥Aθ ∥ et ρ(Aθ).
. Calculer ∥Aθ ∥ et ρ(Aθ).
b) Soient A 
 n(C), λ
n(C), λ  C une valeur propre de A et X = t(x1,…,xn) un vecteur propre
associé. Montrer que |λ||xi|≤
C une valeur propre de A et X = t(x1,…,xn) un vecteur propre
associé. Montrer que |λ||xi|≤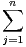 |ai,j||xj| pour tout i. En déduire que ρ(A) ≤∥A∥.
|ai,j||xj| pour tout i. En déduire que ρ(A) ≤∥A∥.
c) Soient A 
 n(C) et k
n(C) et k  N*. Montrer que ρ(Ak) = ρ(A)k.
N*. Montrer que ρ(Ak) = ρ(A)k.
d) Soient A et B dans  n(C). Montrer que ∥AB∥≤∥A∥×∥B∥.
n(C). Montrer que ∥AB∥≤∥A∥×∥B∥.
e) Soit A 
 n (C) diagonalisable. Montrer que Ak → 0 si et seulement si ρ(A) < 1.
n (C) diagonalisable. Montrer que Ak → 0 si et seulement si ρ(A) < 1.
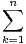
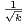 .
.
 N*, gn : x
N*, gn : x
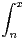 exp(t2)d t.
exp(t2)d t.
a) Montrer que, pour n  N*, il existe un unique xn vérifiant gn(xn) = 1.
N*, il existe un unique xn vérifiant gn(xn) = 1.
b) Trouver un équivalent de xn.
 (N * )2 , un+m ≤ un + um.
(N * )2 , un+m ≤ un + um.
a) Soient α  R et, pour n
R et, pour n  N*, vn = nα. Montrer que (vn) vérifie (*) si et seulement si α ≤ 1.
Déterminer dans ce cas la limite de la suite de terme général vn⁄n.
N*, vn = nα. Montrer que (vn) vérifie (*) si et seulement si α ≤ 1.
Déterminer dans ce cas la limite de la suite de terme général vn⁄n.
b) Soit (wn ) une suite réelle telle que : ∀(n,m)  (N*)2, wn+m = wn + wm. Montrer
qu’une telle suite est arithmétique. Déterminer la limite de la suite de terme général
wn ⁄n.
(N*)2, wn+m = wn + wm. Montrer
qu’une telle suite est arithmétique. Déterminer la limite de la suite de terme général
wn ⁄n.
c) Soit (un ) une suite vérifiant (*). On suppose que la suite de terme général un⁄n
est minorée et on pose : α = inf 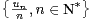 . Montrer que (u
n⁄n) a pour limite
α.
. Montrer que (u
n⁄n) a pour limite
α.
Ind. On pourra fixer ϵ > 0 et considérer q  N* tel que α ≤ uq⁄q ≤ α + ϵ.
N* tel que α ≤ uq⁄q ≤ α + ϵ.
 N telles que
N telles que 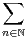 x
x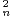 converge.
converge.
a) Pour (a, b) 
 2, montrer que 2|ab|≤ a2 + b2.
2, montrer que 2|ab|≤ a2 + b2.
b) Montrer que E est un sous-espace vectoriel de l’espace des suites numériques réelles.
c) Montrer que f : (xn) 
 N
N x0
x0 
 est une application linéaire.
est une application linéaire.
d) Soit ϕ: ((xn ),(yn))  E2
E2
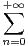 xnyn
xnyn 
 . Montrer que ϕ est un produit scalaire sur E. En
déduire que
. Montrer que ϕ est un produit scalaire sur E. En
déduire que 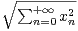 est l’expression d’une norme sur E.
est l’expression d’une norme sur E.
On munit E de cette norme notée N.
e) Montrer que, pour (xn) dans E, la suite (xn + xn+1) est aussi dans E.
f) Soit g: (xn )  E
E (xn + xn+1)
(xn + xn+1)  E. Montrer que g est lipschitzienne pour la norme
N.
E. Montrer que g est lipschitzienne pour la norme
N.
a) On pose Tn = 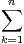 φ(k). Montrer que
φ(k). Montrer que 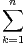
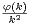 =
= 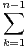 Tk
Tk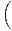
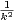 -
-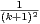
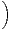 +
+ 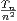 .
.
b) Conclure quant à la convergence de 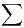
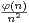 .
.
a) Montrer que (bn) est de signe fixe à partir d’un certain rang.
b) Montrer que les séries de termes généraux an et bn sont de même nature.
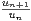 ≤
≤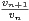 .
.
a) Montrer que un = O(vn).
b) Soit (α, β)  (
( +)2, α ⁄= β. Soit wn =
+)2, α ⁄= β. Soit wn = 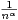 . On suppose que
. On suppose que 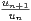 = 1 -
= 1 -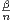 + o
+ o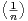 .
.
i) Trouver un équivalent de 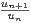 -
-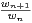 .
.
ii) Montrer que la série de terme général un converge lorsque β > 1, et diverge lorsque β < 1.
b) Pour tout n  N, on pose un = sin(π(2 +
N, on pose un = sin(π(2 + 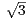 )n). Montrer que, pour tout n
)n). Montrer que, pour tout n  N,
(2 +
N,
(2 + 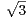 )n + (2 -
)n + (2 -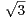 )n est un entier pair. Montrer que un = -sin(π(2 -
)n est un entier pair. Montrer que un = -sin(π(2 -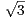 )n) et en déduire que
la série de terme général un converge.
)n) et en déduire que
la série de terme général un converge.
c) Soit P = X3 + a1X2 + a2X + a3  C[X]. On note x1,x2,x3 les racines complexes de P
(éventuellement répétées avec leur ordre de multiplicité). On suppose que |x1| > 1, |x2| < 1 et
|x3 | < 1. On pose σ1 = x1 + x2 + x3, σ2 = x1x2 + x2x3 + x3x1, σ3 = x1x2x3 et, pour n
C[X]. On note x1,x2,x3 les racines complexes de P
(éventuellement répétées avec leur ordre de multiplicité). On suppose que |x1| > 1, |x2| < 1 et
|x3 | < 1. On pose σ1 = x1 + x2 + x3, σ2 = x1x2 + x2x3 + x3x1, σ3 = x1x2x3 et, pour n  N,
Sn = x
N,
Sn = x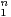 + x
+ x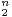 + x
+ x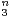 .
.
i) Exprimer a1 ,a2,a3 à l’aide de σ1,σ2,σ3.
ii) Calculer σ1 σ2 - 3σ3.
iii) Exprimer S1,S2,S3 en fonction de σ1,σ2,σ3.
iv) Montrer que, pour p  N, Sp+3 - σ1Sp+2 + σ2Sp+1 - σ1Sp = 0.
N, Sp+3 - σ1Sp+2 + σ2Sp+1 - σ1Sp = 0.
 ]1,+∞[ et (un)n≥1 une suite réelle définie par u1 > 0 et, pour n
]1,+∞[ et (un)n≥1 une suite réelle définie par u1 > 0 et, pour n  N*,
un+1 =
N*,
un+1 = 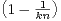 un.
un.
a) tudier la monotonie de (un).
b) La suite (un ) est-elle convergente ?
c) tudier la convergence de 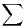 (vn+1 - vn) avec vn = ln(n-1⁄kun).
(vn+1 - vn) avec vn = ln(n-1⁄kun).
d) tudier la convergence de (vn).
e) En déduire un équivalent simple de (un).
f) tudier la convergence des séries de termes généraux un, 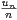 et (-1)nu
n.
et (-1)nu
n.
g) Montrer que la suite de terme général wn = 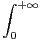
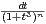 vérifie les conditions de
l’introduction.
vérifie les conditions de
l’introduction.
 ]0,1]
]0,1]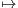
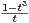 .
.
a) Montrer que ϕ réalise une bijection de ]0,1] sur [0,+∞[. On note u la réciproque de ϕ.
b) Montrer que u est dérivable.
c) Montrer que, pour x  R+*, u(x)3 + xu(x) - 1 = 0. En déduire que : |uʹ(x)|≤
R+*, u(x)3 + xu(x) - 1 = 0. En déduire que : |uʹ(x)|≤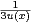 .
.
 R*
R*
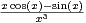 . La fonction g est-elle prolongeable par continuité en
0 ? Ce prolongement est-il de classe
. La fonction g est-elle prolongeable par continuité en
0 ? Ce prolongement est-il de classe  1 ? de classe
1 ? de classe  ∞ ?
∞ ?

 0(R, R) telles que : ∀x
0(R, R) telles que : ∀x 
 , xf(x) = 2
, xf(x) = 2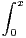 f(t)d t.
f(t)d t.
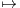
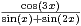 .
.
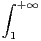
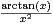 d x.
d x.
 R, n
R, n  N* et fn : x
N* et fn : x  R
R x(1 + nα e-nx).
x(1 + nα e-nx).
a) Étudier la convergence de la suite (fn). Préciser la limite.
b) Pour quelles valeurs de α a-t-on convergence uniforme sur R+ ?
c) Calculer lim n→+∞ x
x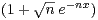 d x.
d x.
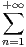 n2xn.
n2xn.
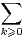 (-1)k
(-1)k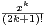 ?
?
 N et Hp : x
N et Hp : x
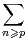
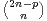
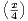 n. Déterminer le rayon de convergence de Hp.
Calculer H0 (x).
n. Déterminer le rayon de convergence de Hp.
Calculer H0 (x).

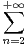
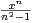 . Déterminer le domaine de définition de f et donner une
expression simple de f(x) pour x
. Déterminer le domaine de définition de f et donner une
expression simple de f(x) pour x  ] - 1,1[.
] - 1,1[.
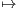
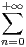
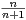 xn ?
xn ?

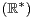 2 et f : x
2 et f : x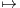
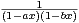 . Déterminer le développement en série
entière de f au voisinage de 0 et préciser le rayon de convergence.
. Déterminer le développement en série
entière de f au voisinage de 0 et préciser le rayon de convergence.
b) Soit (an ) une suite telle que la série de terme général an converge. Que dire du rayon de convergence de la série entière de terme général anzn ?
c) Calculer le rayon de convergence de la série entière 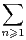 (-1)n ln
(-1)n ln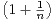 zn.
zn.

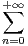 (3n + 1)2xn.
(3n + 1)2xn.
a) Déterminer le rayon de convergence de S.
b) Montrer, pour |x| < 1 : S(x) = 9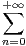 (n + 1)(n + 2)xn - 21
(n + 1)(n + 2)xn - 21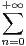 (n + 1)xn + 4
(n + 1)xn + 4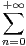 xn.
xn.
c) En déduire les solutions de S(x) = 0.
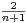 an-1⋅
an-1⋅
a) Montrer que 1 ≤ an ≤ n2 pour tout n  N*.
N*.
b) Déterminer le rayon de convergence R de la série entière 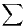 anxn.
anxn.
c) Soit f : x  ] - R,R[
] - R,R[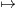
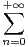 anxn.
anxn.
i) Montrer que f est solution de l’équation différentielle (1 - x)yʹ- (1 + 2x)y = 0.
ii) Donner une expression de f à l’aide de fonctions usuelles.
 N, on pose In =
N, on pose In = 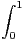
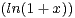 n d x.
n d x.
a) Justifier la définition de In. Montrer que, pour n  N, 0 ≤ In ≤ (ln2)n.
N, 0 ≤ In ≤ (ln2)n.
b) Montrer que, pour n  N, In+1 = 2(ln2)n+1 - (n + 1)In.
N, In+1 = 2(ln2)n+1 - (n + 1)In.
c) Montrer que la série de terme général 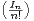 n converge. Calculer
n converge. Calculer 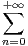
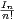 .
.
d) Déterminer le rayon de convergence et la somme de x
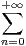
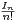 xn.
xn.
e) Montrer que In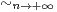
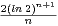 .
.
 N, un+1 =
N, un+1 = 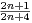 un.
un.
a) Montrer que (un) est décroissante et que (un) converge.
b) Soit vn = 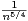 .
.
i) Montrer que 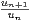 -
-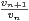 = -
= -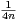 + o
+ o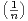 .
.
ii) Montrer qu’il existe un entier N tel que, pour tout n ≥ N, on a 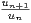 ≤
≤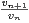 . En déduire
qu’il existe un K
. En déduire
qu’il existe un K  R
R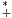 tel que, pour tout n
tel que, pour tout n  N, un ≤ Kvn.
N, un ≤ Kvn.
iii) Montrer que la série de terme général un converge.
c) En remarquant que 2(k + 1)uk+1 + 2uk+1 = 2kuk + uk, déterminer la valeur de la somme de la série des uk .
d) Soit f : x
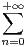 unxn.
unxn.
i) Montrer que le rayon de convergence R de cette série entière est > 0.
ii) Montrer que f vérifie l’équation (E): 2x(x - 1)fʹ(x) + (x - 2)f(x) = -2.
iii) Résoudre l’équation différentielle (E) pour x  ] - R,R[.
] - R,R[.
Ind. On a : ∀x 
 \{0,1},
\{0,1}, 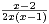 =
= 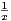 -
-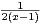 .
.
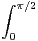
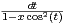 .
.
a) Montrer que F est définie sur ] - 1,1[.
b) Pour N  N* et (x,t)
N* et (x,t)  ] - 1,1[×[0,π⁄2], montrer :
] - 1,1[×[0,π⁄2], montrer :
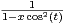 =
= 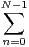 (xcos2(t))n +
(xcos2(t))n + 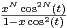 .
.
c) Montrer que ∀x  ] - 1,1[, F(x) =
] - 1,1[, F(x) = 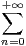 Wnxn, où Wn est une intégrale à déterminer.
Wnxn, où Wn est une intégrale à déterminer.
d) Montrer que, pour x  ] - 1,1[, F(x) =
] - 1,1[, F(x) = 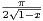 .
.
e) En déduire la valeur de Wn.
 N, on pose In =
N, on pose In = 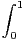 xxn
d x. Étudier la convergence de la suite
(In ).
xxn
d x. Étudier la convergence de la suite
(In ).
 N*, soit fn : t
N*, soit fn : t  R+
R+
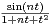 .
.
a) La fonction fn est-elle intégrable sur  + ?
+ ?
b) Calculer lim n→+∞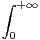 fn(t)d t.
fn(t)d t.
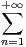
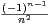 =
= 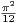 . Pour n ≥ 1, on pose un =
. Pour n ≥ 1, on pose un = 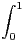 ln(1 + tn)d t.
ln(1 + tn)d t.
a) Donner le développement en série entière de t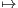 ln(1 + t) au voisinage de zéro.
ln(1 + t) au voisinage de zéro.
b) Montrer que un = 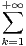
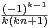 .
.
c) Montrer que f : x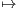
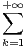
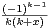 est de classe
est de classe  1.
1.
d) Exprimer un en fonction de f et en déduire que un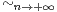
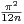 .
.
e) Montrer que l’on a, lorsque n → +∞ : un = 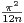 +
+ 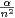 + o
+ o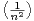 où α s’écrit comme la somme
d’une série.
où α s’écrit comme la somme
d’une série.
f) Chercher a, b, c,d tels que 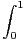
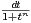 = a +
= a + 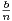 +
+ 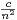 +
+ 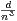 + o
+ o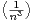 .
.

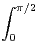 Arctan
Arctan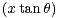 d θ.
d θ.
a) Montrer que, pour x  R+*, Arctan(x) + Arctan(1⁄x) = π⁄2.
R+*, Arctan(x) + Arctan(1⁄x) = π⁄2.
b) Montrer que f est définie sur R et de classe  1. Déterminer son sens de variations.
1. Déterminer son sens de variations.
c) Montrer que, pour x  R+*, f(x) + f(1⁄x) = π2⁄4. En déduire la limite de f en
+ ∞.
R+*, f(x) + f(1⁄x) = π2⁄4. En déduire la limite de f en
+ ∞.

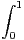
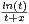 d t.
d t.
a) Montrer que f est définie sur R+*.
b) Soit t  ]0, 1[. Exprimer
]0, 1[. Exprimer 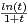 comme somme d’une série.
comme somme d’une série.
c) On rappelle que 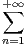
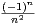 = -
= -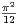 . Calculer f(1).
. Calculer f(1).
d) Montrer que, pour x  R+*, f(x) = ln(x) × ln
R+*, f(x) = ln(x) × ln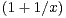 +
+ 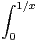
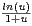 d u.
d u.
e) Donner une expression de fʹ(x) ne faisant pas intervenir d’intégrale.
f) Soit g : x  R +*
R +* f(x) + f(1⁄x). Montrer que g est de classe
f(x) + f(1⁄x). Montrer que g est de classe  1. Montrer que gʹ(x) = -
1. Montrer que gʹ(x) = -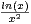 pour x
pour x  R +* .
R +* .
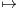
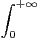 exp(-t2)cos(xt)d t.
exp(-t2)cos(xt)d t.
a) Montrer que f est définie sur  , puis que f est de classe
, puis que f est de classe  1.
1.
b) Montrer que f vérifie une équation différentielle. Résoudre cette équation différentielle et en déduire une expression de f.

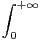
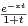 d t. Montrer que F est définie sur R+*.
d t. Montrer que F est définie sur R+*.
b) Montrer que F est positive et décroissante.
c) Montrer que F est de classe  1 sur R+*. Calculer F -Fʹ ;endéduirequeF est de classe
1 sur R+*. Calculer F -Fʹ ;endéduirequeF est de classe  ∞
sur R +* .
∞
sur R +* .
d) Montrer : ∀x  R+*, F(x) = ex
R+*, F(x) = ex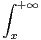
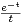 d t. Calculer la limite de F(x) quand x tend vers
0+ .
d t. Calculer la limite de F(x) quand x tend vers
0+ .
e) Donner un équivalent de F(x) quand x tend vers 0+.
 à valeurs réelles. On dit que f est
2-convexe si f est de classe
à valeurs réelles. On dit que f est
2-convexe si f est de classe  2 et fʹʹ≥ 0.
2 et fʹʹ≥ 0.
a) Si f est 2-convexe, montrer que exp(f) l’est aussi.
b) Soit Γ : x
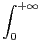 tx-1e-t d t.
tx-1e-t d t.
i) Montrer que Γ est définie sur ]0,+∞[ et que H est strictement positive.
ii) Montrer que H est de classe  2 et 2-convexe.
2 et 2-convexe.
iii) On admet que, pour tout x > 0, Γ(x + 1) = xΓ(x). Montrer qu’il existe c  ]1,2[ tel que
Γʹ(c) = 0. tudier les variations de Γ et ses limites en 0 et + ∞.
]1,2[ tel que
Γʹ(c) = 0. tudier les variations de Γ et ses limites en 0 et + ∞.
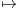
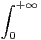
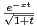 d t.
d t.
b) Montrer que f est solution d’une équation différentielle que l’on précisera.
 R, on pose f(x) =
R, on pose f(x) = 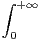
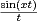 e-t d t.
e-t d t.
a) Si x  R , montrer que
R , montrer que 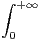 cos(xt)e-t d t existe.
cos(xt)e-t d t existe.
b) Montrer que 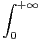 cos(xt)e-t d t =
cos(xt)e-t d t = 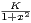 avec K indépendant de x.
avec K indépendant de x.
c) Montrer que 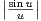 ≤ 1 pour u
≤ 1 pour u  R* et en déduire l’existence de f.
R* et en déduire l’existence de f.
d) Montrer que f est de classe  1. Déterminer fʹ puis f.
1. Déterminer fʹ puis f.
e) Soit L : x  R +
R +
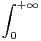
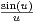 e-ux d u. Montrer l’existence de L. En supposant que L est
continue en 0, calculer L(0).
e-ux d u. Montrer l’existence de L. En supposant que L est
continue en 0, calculer L(0).

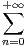
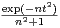 .
.
a) Montrer que f est définie et continue sur  .
.
b) Montrer que pour tout t dans  +*, 0 ≤ f(t) - 1 ≤
+*, 0 ≤ f(t) - 1 ≤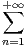 exp(-nt2), et en déduire que
lim+∞f = 1.
exp(-nt2), et en déduire que
lim+∞f = 1.
c) Montrer que f est de classe  1 sur
1 sur  . tudier les variations de f.
. tudier les variations de f.
d) Montrer que 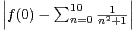 ≤
≤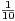 .
.

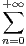 e-xn2
.
e-xn2
.
a) Déterminer le domaine de définition de f. Montrer que la série de fonctions ne converge pas
normalement sur  +*.
+*.
b) Montrer que f est continue sur  +*.
+*.
c) Montrer que f - 1 est intégrable sur  +*. Exprimer
+*. Exprimer 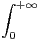 (f - 1) en fonction de
(f - 1) en fonction de
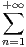
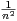 .
.
d) On admet que, pour x > 0, on a : 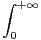 exp(-xt2)d t ≤ f(x) ≤ 1 +
exp(-xt2)d t ≤ f(x) ≤ 1 + 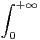 exp(-xt2)d t.
Déterminer un équivalent de f en 0+.
exp(-xt2)d t.
Déterminer un équivalent de f en 0+.
e) Démontrer l’encadrement admis à la question précédente.
 [0,1]
[0,1]
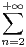
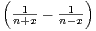 . Montrer que F est définie et continue.
Calculer
. Montrer que F est définie et continue.
Calculer 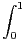 F(x)d x.
F(x)d x.
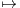
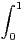
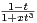 d t et D = [-1,+∞[.
d t et D = [-1,+∞[.
a) Montrer que f est définie et continue sur D.
b) Montrer que f est développable en série entière au voisinage de 0 et déterminer ce développement.
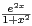 .
.
a) Donner les solutions de l’équation homogène.
b) Donner les solutions de (E).
a) Donner une condition sur α pour que y: x exp(αx) soit solution de (E).
exp(αx) soit solution de (E).
On choisit désormais un tel α.
b) Donner une condition sur z pour que y: x z(x)exp(αx) soit solution de (E).
z(x)exp(αx) soit solution de (E).
c) En déduire les solutions de (E).
 +*.
+*.
a) Trouver α tel que la fonction hα: x 
 +*
+* xα soit solution de (E).
xα soit solution de (E).
b) Soit G: x 
 +*
+*
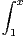
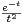 d t. Donner le tableau de variations de G. Quelle est sa limite en
zéro ?
d t. Donner le tableau de variations de G. Quelle est sa limite en
zéro ?
c) Soit f : R +* → R deux fois dérivable. Montrer que s: x 
 +*
+* xf(x) est solution de (E) si
et seulement si fʹ est solution d’une équation différentielle linéaire d’ordre 1 notée (Eʹ) que l’on
déterminera. Résoudre (Eʹ) sur
xf(x) est solution de (E) si
et seulement si fʹ est solution d’une équation différentielle linéaire d’ordre 1 notée (Eʹ) que l’on
déterminera. Résoudre (Eʹ) sur  +*.
+*.
d) Décrire l’ensemble des solutions de (E) à l’aide de G. Déterminer le comportement des solutions lorsque x → 0+.
 centré en zéro, ϕ
centré en zéro, ϕ 
 ∞(I, R) une fonction paire et (E)
l’équation différentielle yʹʹ(x) + ϕ(x)y(x) = 0. Soit y une solution de (E). Montrer que y est de
classe
∞(I, R) une fonction paire et (E)
l’équation différentielle yʹʹ(x) + ϕ(x)y(x) = 0. Soit y une solution de (E). Montrer que y est de
classe  ∞ et que la fonction x
∞ et que la fonction x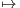 y(-x) est également solution de (E).
y(-x) est également solution de (E).
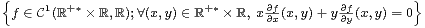 .
.
a) Soit g 
 1 (
1 ( ,
,  ). On pose ∀(x,y)
). On pose ∀(x,y) 
 +*×
+*×  , f(x,y) = g(y⁄x). Montrer que
f
, f(x,y) = g(y⁄x). Montrer que
f  E.
E.
b) Soient f  E et v
E et v 
 . On pose ∀t
. On pose ∀t 
 +*, ϕ(t) = f(t,vt). Montrer que ϕ est de classe
+*, ϕ(t) = f(t,vt). Montrer que ϕ est de classe  1 et
que ϕʹ est la fonction nulle.
1 et
que ϕʹ est la fonction nulle.
c) Soit f une fonction de  +*×
+*×  dans
dans  . Déduire des questions précédentes l’équivalence
suivante : f
. Déduire des questions précédentes l’équivalence
suivante : f  E⇐⇒∃g
E⇐⇒∃g 
 1(
1( ),∀(x,y)
),∀(x,y) 
 +*×
+*×  , f(x,y) = g(y⁄x).
, f(x,y) = g(y⁄x).
 N*, Sn =
N*, Sn = 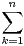 k.
k.
a) Montrer que, pour tout n  N, il existe un unique p
N, il existe un unique p  N tel que S(p) ≤ n < S(p + 1).
N tel que S(p) ≤ n < S(p + 1).
b) Soient A et B deux ensembles dénombrables, (xi)i N et (yj)j
N et (yj)j N deux énumérations de A et B
respectivement. Montrer que l’application ψ: (xi,yj)
N deux énumérations de A et B
respectivement. Montrer que l’application ψ: (xi,yj)
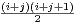 + i est une bijection de
A × B sur N.
+ i est une bijection de
A × B sur N.
c) Que peut-on en conclure ?
 N avec n ≥ 2, (Ω,
N avec n ≥ 2, (Ω,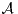 ,P) un espace probabilisé et (Ai)1≤i≤n un
système complet d’évènements tel que (P(Ai))1≤i≤n soit une suite arithmétique avec
P(A1 ) =
,P) un espace probabilisé et (Ai)1≤i≤n un
système complet d’évènements tel que (P(Ai))1≤i≤n soit une suite arithmétique avec
P(A1 ) = 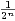 .
.
a) Exprimer P(Ai) pour tout i.
b) On considère un évènement B tel que, pour tout i  {1,…,n}, P(B|Ai) =
{1,…,n}, P(B|Ai) = 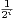 . Exprimer
P(B).
. Exprimer
P(B).
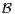 (n, p) et
(n, p) et 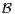 (m,p).
(m,p).
a) Donner la fonction génératrice de X.
b) Donner la fonction génératrice de X + Y , puis sa loi.
 N. Déterminer la loi conditionnelle de X sachant
(X + Y = n).
N. Déterminer la loi conditionnelle de X sachant
(X + Y = n).
 N* une suite de variables aléatoires indépendantes identiquement
distribuées et suivant une loi de Bernoulli de paramètre p
N* une suite de variables aléatoires indépendantes identiquement
distribuées et suivant une loi de Bernoulli de paramètre p  ]0,1[.
]0,1[.
On pose N = inf {n  N*, Xn = 1} si cet ensemble est non vide, N = +∞ sinon.
N*, Xn = 1} si cet ensemble est non vide, N = +∞ sinon.
a) Calculer P(N = +∞).
b) Donner la loi de N.
[Épreuves orales des concours]

