[Épreuves orales des concours]Algèbre
a) On suppose que, pour tout x  R, P(x) + Pʹ(x) ≥ 0. Montrer que P(x) ≥ 0 pour tout
x
R, P(x) + Pʹ(x) ≥ 0. Montrer que P(x) ≥ 0 pour tout
x  R .
R .
b) On suppose maintenant que, pour tout x  R, P(x) -Pʹʹ(x) ≥ 0. Montrer que P(x) ≥ 0 pour
tout x
R, P(x) -Pʹʹ(x) ≥ 0. Montrer que P(x) ≥ 0 pour
tout x  R .
R .
c) On suppose ici que, pour tout x  R, P(x) - Pʹ(x) - Pʹʹ(x) + Pʹʹʹ(x) ≥ 0. Peut-on dire que
P(x) ≥ 0 pour tout x
R, P(x) - Pʹ(x) - Pʹʹ(x) + Pʹʹʹ(x) ≥ 0. Peut-on dire que
P(x) ≥ 0 pour tout x  R ?
R ?
 n(R). Montrer que, si A ou B est inversible alors
A + tB est inversible pour tout réel t, sauf un nombre fini de valeurs de t.
n(R). Montrer que, si A ou B est inversible alors
A + tB est inversible pour tout réel t, sauf un nombre fini de valeurs de t.
b) Soient 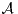 = (a1,…,an) et
= (a1,…,an) et 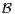 = (b1,…,bn) deux familles de vecteurs de Rn. Montrer que, si
= (b1,…,bn) deux familles de vecteurs de Rn. Montrer que, si 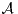 ou
ou
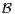 est libre alors la famille
est libre alors la famille  = (a1 + tb1,
= (a1 + tb1, ,an + tbn) est libre pour tout réel t, sauf un nombre
fini de valeurs de t.
,an + tbn) est libre pour tout réel t, sauf un nombre
fini de valeurs de t.
 K, ∀x
K, ∀x  E, f(x) = λx.
E, f(x) = λx.
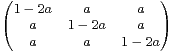 de
de  3 (R ).
3 (R ).
a) Montrer que, pour tous a,b  R, M(a)M(b) = M(a + b - 3ab).
R, M(a)M(b) = M(a + b - 3ab).
b) quelle(s) condition(s) la matrice M(a) est-elle inversible ?
c) Trouver une suite (un) telle que M(a)n = M(un) pour tout n  N.
N.
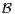 . On note P le plan
d’équation x + y + z = 0, D la droite d’équations x =
. On note P le plan
d’équation x + y + z = 0, D la droite d’équations x = 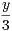 =
= 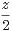 , et p la projection sur P
parallèlement à D.
, et p la projection sur P
parallèlement à D.
a) Montrer que P ⊕ D = R3.
b) Soit u un vecteur de R3 de coordonnées (x,y,z) dans  . Calculer p(u) et déterminer la matrice
de p dans
. Calculer p(u) et déterminer la matrice
de p dans  .
.
 .
Montrer que pour tout entier n ≥ 1, An est combinaison linéaire de A et A2. Calculer
An .
.
Montrer que pour tout entier n ≥ 1, An est combinaison linéaire de A et A2. Calculer
An .
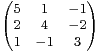 .
.
a) Montrer que A est diagonalisable.
b) Calculer An .
c) Soient u0 = v0 = w0 = 1 et ∀n  N,
N, 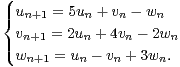
Pour n  N, calculer un, vn, wn.
N, calculer un, vn, wn.
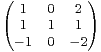 .
.
a) Diagonaliser A (donner P  GL3(R) et D diagonale telles que A = PDP-1).
GL3(R) et D diagonale telles que A = PDP-1).
b) Soit (α, β)  R2. La matrice αA + βIn est-elle diagonalisable ?
R2. La matrice αA + βIn est-elle diagonalisable ?
 N*, E un espace vectoriel de dimension n, x0
N*, E un espace vectoriel de dimension n, x0  E non nul et ϕ une forme
linéaire non identiquement nulle sur E. On définit u sur E par u(x) = x + ϕ(x)x0.
E non nul et ϕ une forme
linéaire non identiquement nulle sur E. On définit u sur E par u(x) = x + ϕ(x)x0.
a) Montrer que u est un endomorphisme de E.
b) Montrer que 1 est une valeur propre de u et déterminer l’espace propre associé.
c) Déterminer une condition nécessaire et suffisante pour que u soit diagonalisable. Déterminer son spectre et ses vecteurs propres.
 E, on pose d(P) = Pʹ.
E, on pose d(P) = Pʹ.
a) Montrer que d est un endomorphisme de E.
b) Trouver le noyau et l’image de d.
c) L’endomorphisme d est-il diagonalisable ?
 Rn[X]
Rn[X]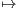 Pʹ- XPʹʹ
Pʹ- XPʹʹ
a) Monter que u est un endomorphisme de  n[X].
n[X].
b) Trouver la seule valeur propre possible λ de u.
c) L’endomorphisme u est-il diagonalisable ? inversible ?
d) Calculer le sous-espace propre de λ.
 Rn[X], g(P) = n2XP - (X2 + X)Pʹ- X3Pʹʹ.
Rn[X], g(P) = n2XP - (X2 + X)Pʹ- X3Pʹʹ.
a) Montrer que g est un endomorphisme de Rn[X].
b) Montrer que g est diagonalisable.
c) L’application g est-elle inversible ?
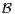 et f l’endomorphisme
dont la matrice dans
et f l’endomorphisme
dont la matrice dans 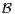 est A =
est A =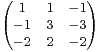 .
.
a) Montrer que E = Ker(f2) ⊕ Ker(f - 2IdE).
b) Donner un élément de Ker(f2) \ Ker(f).
c) Montrer qu’il existe une base 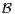 ʹ de E telle que Mat
ʹ de E telle que Mat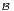 ʹ(f) =
ʹ(f) =  .
.
d) Soit g 
 (E) tel que g2 = f. Montrer que Ker(f2) est stable par g. Qu’en déduire ?
(E) tel que g2 = f. Montrer que Ker(f2) est stable par g. Qu’en déduire ?
 3(C) telle que M soit semblable à 2M.
3(C) telle que M soit semblable à 2M.
a) Quelles sont les valeurs propres de M ? Montrer que M est semblable à une matrice triangulaire supérieure à diagonale nulle.
b) On suppose M de rang 1. Montrer qu’elle est semblable à  .
.
 R et A =
R et A =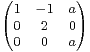 . Déterminer le rang de A. La matrice A est-elle diagonalisable ? Pour a = 1, calculer
An .
. Déterminer le rang de A. La matrice A est-elle diagonalisable ? Pour a = 1, calculer
An .
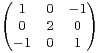 et f l’endomorphisme de R3 canoniquement associé à A.
et f l’endomorphisme de R3 canoniquement associé à A.
a) Trouver les valeurs propres de f. Cet endomorphisme est-il diagonalisable ?
b) Soit (a, b)  R2. Trouver les valeurs propres de g = af + bid.
R2. Trouver les valeurs propres de g = af + bid.
c) quelles conditions sur (a,b) l’endomorphisme g est-il bijectif ?
 C3 \{0} et M =
C3 \{0} et M =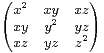 .
.
a) Montrer qu’il existe C 
 3,1(C) tel que M = CCT.
3,1(C) tel que M = CCT.
b) Déterminer le rang de M.
c) Montrer que M est semblable à une matrice de la forme N = avec (a, b, c)≠ (0, 0,0). Expliciter a en fonction de x, y et z.
avec (a, b, c)≠ (0, 0,0). Expliciter a en fonction de x, y et z.
d) En déduire une condition nécessaire et suffisante pour que M soit diagonalisable.
 C3, M =
C3, M =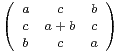 et K =
et K = .
.
a) Diagonaliser K.
b) Exprimer M à l’aide des puissances de K.
c) Montrer que M est diagonalisable.
 . La matrice A est elle diagonalisable ? Déterminer la limite de An quand n tend vers
l’infini.
. La matrice A est elle diagonalisable ? Déterminer la limite de An quand n tend vers
l’infini.
a) Calculer le rang de C, le noyau de C et l’image de C. Qu’en déduit-on sur les valeurs propres ?
b) Calculer C2 . Montrer que si a est valeur propre de C alors a2 est valeur propre de C2 .
c) En déduire les valeurs propres de C.
 .
Déterminer le rang de A. Montrer que A est diagonalisable et préciser ses éléments
propres.
.
Déterminer le rang de A. Montrer que A est diagonalisable et préciser ses éléments
propres.

 6(R) inversible et vérifiant A3 - 3A2 + 2A = 0 ainsi que tr(A) = 8.
6(R) inversible et vérifiant A3 - 3A2 + 2A = 0 ainsi que tr(A) = 8.
a) Montrer que A est diagonalisable.
b) Que peut-on dire sur les valeurs propres de A ?
c) Donner une matrice diagonale semblable à A.
d) Déterminer l’ensemble des polynômes annulateurs de A.
 2(R) →
2(R) → 2(R), M =
2(R), M = 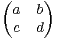
 .
.
a) Montrer que f est un endomorphisme de  2(R).
2(R).
b) Déterminer les éléments propres de f.
c) L’endomorphisme f est-il diagonalisable ? est-il inversible ?

 n(C)
n(C) M + tr(M)In.
M + tr(M)In.
a) Montrer que ϕ est un endomorphisme de  n(C).
n(C).
b) Trouver le noyau et le rang de ϕ.
c) Trouver un polynôme annulateur de ϕ de degré 2.
d) L’endomorphisme ϕ est-il diagonalisable ?
e) L’endomorphisme ϕ est-il inversible ? Si oui, trouver son inverse.
 P - Pʹ.
P - Pʹ.
a) Montrer que l’endomorphisme f est bijectif.
b) Est-il diagonalisable ?
c) Soient g un endomorphisme nilpotent d’un espace vectoriel E et p un entier tel que gp = 0.
Montrer que id E - g est bijectif et que (idE - g)-1 = idE + g +  + gp-1.
+ gp-1.
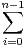 αiXi avec α0 > 0 et αi ≥ 0 pour 1 ≤ i < n.
αiXi avec α0 > 0 et αi ≥ 0 pour 1 ≤ i < n.
a) Montrer que P admet une unique racine sur R+*. Ind. Considérer P(X)⁄Xn.
b) Soit M 
 n(R) définie par : Mi,1 = i pour 1 ≤ i ≤ n, Mi,i+1 = 1 pour 1 ≤ i < n, et tous
les autres coefficients nuls. Montrer que M admet une unique valeur propre strictement
positive.
n(R) définie par : Mi,1 = i pour 1 ≤ i ≤ n, Mi,i+1 = 1 pour 1 ≤ i < n, et tous
les autres coefficients nuls. Montrer que M admet une unique valeur propre strictement
positive.

 (E), φ(u) =
(E), φ(u) = 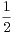 (s • u + u • s).
(s • u + u • s).
a) Montrer que φ est un endomorphisme de  (E)
(E)
b) Calculer φ3 et en déduire un polynôme annulateur de φ.
c) L’endomorphisme φ est-il diagonalisable ?
 Rn[X], on définit U(P) : x
Rn[X], on définit U(P) : x ex
ex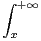 e-tP(t)d t.
e-tP(t)d t.
a) Montrer que U est un endomorphisme de Rn[X].
b) Cet endomorphisme est-il diagonalisable ? inversible ? Si oui, déterminer son inverse.

 n(R) telle que A3 = A + I. Montrer que A est inversible, puis que
det(A) > 0.
n(R) telle que A3 = A + I. Montrer que A est inversible, puis que
det(A) > 0.

 n(C) vérifiant M2 + tM = In.
n(C) vérifiant M2 + tM = In.
a) On suppose que M est symétrique. Montrer que M est diagonalisable puis prouver que tr (M) det (M)≠0.
b) Montrer que M est diagonalisable même si elle n’est pas symétrique.
c) Montrer que M est inversible si et seulement si 1 n’est pas valeur propre de M.
 n(C) peut se décomposer comme somme d’une matrice
triangulaire supérieure et d’une matrice triangulaire inférieure.
n(C) peut se décomposer comme somme d’une matrice
triangulaire supérieure et d’une matrice triangulaire inférieure.
b) Montrer qu’on peut choisir ces deux matrices inversibles.
c) Montrer que toute matrice de  n(C) peut se décomposer comme somme de deux matrices
diagonalisables.
n(C) peut se décomposer comme somme de deux matrices
diagonalisables.
d) Montrer que toute matrice triangulaire  n(C) est limite d’une suite de matrices
inversibles.
n(C) est limite d’une suite de matrices
inversibles.
 GLn(R). La matrice Q =
GLn(R). La matrice Q =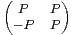 est-elle inversible ? Si oui, donner son inverse.
est-elle inversible ? Si oui, donner son inverse.
b) Soit A 
 n (R) une matrice possédant n valeurs propres positives distinctes. Donner le
polynôme caractéristique de B =
n (R) une matrice possédant n valeurs propres positives distinctes. Donner le
polynôme caractéristique de B =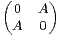 .
La matrice B est-elle diagonalisable ?
.
La matrice B est-elle diagonalisable ?
c) Soient En = diag(1,2,...,n) et Kn =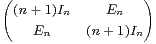 .
Calculer det (Kn ).
.
Calculer det (Kn ).

 n(R) vérifiant 3A3 = A2 + A + In.
n(R) vérifiant 3A3 = A2 + A + In.
a) La matrice A est-elle inversible ? Si oui, donner A-1.
b) Est-elle diagonalisable ?
 n(C) ayant au moins une valeur propre commune.
n(C) ayant au moins une valeur propre commune.
i) Montrer qu’il existe α  C et X,Y
C et X,Y  Cn non nuls, tels que tAX = αX et BY = αY . En
déduire qu’il existe M
Cn non nuls, tels que tAX = αX et BY = αY . En
déduire qu’il existe M 
 n(C) non nulle telle que MA = BM.
n(C) non nulle telle que MA = BM.
ii) Trouver M pour A = 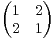 et B =
et B = 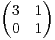 .
.
b) On s’intéresse maintenant à la réciproque. Soient A,B,M dans  n(C) telles que
MA = BM.
n(C) telles que
MA = BM.
i) Montrer que si M est inversible alors A et B ont une valeur propre commune.
ii) Montrer que pour tout P  C[X], on a MP(A) = P(B)M.
C[X], on a MP(A) = P(B)M.
iii) On suppose M≠0. Montrer que A et B ont au moins une valeur propre commune.

 n(C) et M =
n(C) et M = 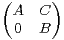 .
.
a) Soient k  N et P
N et P  C[X]. Déterminer les blocs diagonaux de Mk et P(M).
C[X]. Déterminer les blocs diagonaux de Mk et P(M).
b) On suppose que Sp(A) = {λ} et Sp(B) = {μ}, avec λ≠μ. Donner une condition nécessaire et suffisante pour que M soit diagonalisable.
c) Même question dans le cas où λ = μ.
 Rn[X], on pose ϕ(P,Q) =
Rn[X], on pose ϕ(P,Q) = 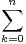 P(k)Q(k).
P(k)Q(k).
a) Montrer que ϕ est un produit scalaire.
b) Trouver une base orthonormale de R3[X] pour ce produit scalaire.
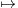 ⟨P,Q⟩ =
⟨P,Q⟩ = 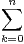 P(k)(1)Q(k)(1).
P(k)(1)Q(k)(1).
a) Montrer que c’est un produit scalaire.
b) Montrer que l’ensemble E = {P  Rn[X],P(1) = 0} est un sous-espace vectoriel de Rn[X] et
donner sa dimension.
Rn[X],P(1) = 0} est un sous-espace vectoriel de Rn[X] et
donner sa dimension.
c) Calculer d(1, E).
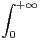 P(t)Q(t)e-t d t.
P(t)Q(t)e-t d t.
a) Montrer que l’on définit ainsi un produit scalaire sur R[X].
b) Déterminer min(a,b) R2
R2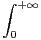 (t2 - at - b)2e-t d t.
(t2 - at - b)2e-t d t.
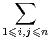 ai,jbi,j.
ai,jbi,j.
a) Montrer que φ est un produit scalaire sur  n(R).
n(R).
b) Soit H l’ensemble des matrices de  n(R) dont la somme des coefficients est nulle. Soit A une
matrice de
n(R) dont la somme des coefficients est nulle. Soit A une
matrice de  n (R). Calculer la distance d(A,H).
n (R). Calculer la distance d(A,H).
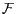 = (x1 , ...,xn) et
= (x1 , ...,xn) et 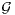 = (y1,...,yn) deux familles de vecteurs de E telles que :
∀(i, j)
= (y1,...,yn) deux familles de vecteurs de E telles que :
∀(i, j)  {1, ..., n}2, (xi|xj) = (yi|yj).
{1, ..., n}2, (xi|xj) = (yi|yj).
a) Montrer que 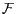 est libre si et seulement si
est libre si et seulement si 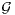 est libre.
est libre.
b) Montrer que dimV ect(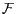 ) = ⌈⟩⇕
) = ⌈⟩⇕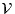 ⌉⌋⊔(
⌉⌋⊔(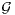 ).
).
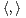 ) un espace euclidien de dimension n et
) un espace euclidien de dimension n et 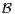 = (e1,...,en) une base
orthonormale de E. Soit f
= (e1,...,en) une base
orthonormale de E. Soit f  GL(E) un automorphisme tel que : ∀(x,y)
GL(E) un automorphisme tel que : ∀(x,y)  E2,
E2, 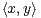 = 0 ⇒
= 0 ⇒
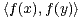 = 0.
= 0.
a) Que dire de la famille 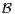 ʹ = (f(e1),...,f(en)) ?
ʹ = (f(e1),...,f(en)) ?
b) En calculant 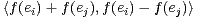 de deux façons, montrer qu’il existe a > 0 tel que
∥f(ei ) ∥2 = a2 pour tout i. Que dire de la famille
de deux façons, montrer qu’il existe a > 0 tel que
∥f(ei ) ∥2 = a2 pour tout i. Que dire de la famille 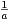
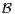 ʹ ?
ʹ ?
 1([0,1]). Pour f,g
1([0,1]). Pour f,g  E, on pose
E, on pose 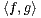 =
= 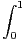 (fg + fʹgʹ). On considère les
sous-espaces V = {f
(fg + fʹgʹ). On considère les
sous-espaces V = {f 
 2([0,1]),fʹʹ = f}, W = {f
2([0,1]),fʹʹ = f}, W = {f  E,f(0) = f(1) = 0}.
E,f(0) = f(1) = 0}.
a) Montrer que la famille (ch,sh) est une base de V .
b) Soient f  V et g
V et g  E. Montrer que
E. Montrer que 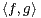 = fʹ(1)g(1) - fʹ(0)g(0).
= fʹ(1)g(1) - fʹ(0)g(0).
c) Soient f  V et g
V et g  W . Montrer que
W . Montrer que 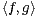 = 0.
= 0.
d) Soit f  E tel que f(0) = 0, f(1) = ch1. Calculer
E tel que f(0) = 0, f(1) = ch1. Calculer 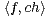 ,
, 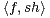 , ∥ch∥2 et ∥sh∥2. En
déduire le projeté orthogonal de f sur V .
, ∥ch∥2 et ∥sh∥2. En
déduire le projeté orthogonal de f sur V .
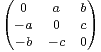

 3 (R ). On pose B = tAA.
3 (R ). On pose B = tAA.
a) Montrer que B n’est pas inversible.
b) Montrer que B est diagonalisable.
c) Montrer que 0  Sp(B) et que Sp(B) ⊂ R+.
Sp(B) et que Sp(B) ⊂ R+.
d) La matrice A est-elle orthogonale ?
e) Montrer que A et B commutent.
f) Montrer que si λ  SpC(A) alors - λ
SpC(A) alors - λ  SpC(A).
SpC(A).

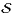 2(R)2, B
2(R)2, B 
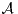 2(R) et M =
2(R) et M =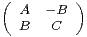 .
.
a) Montrer que M est diagonalisable dans  4(R).
4(R).
b) On prend ici B = 0. Trouver une base de vecteurs propres de M exprimée à partir des vecteurs propres de A et de C.
c) On suppose que G 
 2(R) et E
2(R) et E  GL2(R). Montrer que rg(EG) = rg(GE) = rg(G).
GL2(R). Montrer que rg(EG) = rg(GE) = rg(G).
d) On suppose A inversible et on note P =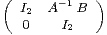 . Calculer MP.
. Calculer MP.
e) En déduire le rang de M.
 ω ∧ x.
ω ∧ x.
a) Montrer que f est un endomorphisme et que, pour tous x,y  R3,
R3, 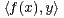 = -
= -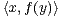 .
.
b) Trouver un polynôme annulateur de f. Cet endomorphisme est-il diagonalisable ?
c) Montrer que l’endomorphisme (f - Id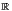 3) • (f + Id
3) • (f + Id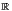 3)-1 est bien défini et déterminer ses
propriétés géométriques.
3)-1 est bien défini et déterminer ses
propriétés géométriques.
 E. Déterminer les réels α tels que x
E. Déterminer les réels α tels que x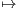 α
α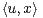 u-x
soit une isométrie de E.
u-x
soit une isométrie de E.

 n,m(R) de rang m.
n,m(R) de rang m.
a) Montrer que : ∀X 
 n,1(R) \{0}, tXAX > 0
n,1(R) \{0}, tXAX > 0
b) Justifier que m ≤ n. Que peut-on dire de l’application linéaire u canoniquement associée à B ?
c) Montrer que la matrice par blocs C = 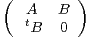 est inversible.
est inversible.
d) Calculer C-1 lorsque m = n.
a) Montrer que f • s • f-1 est une symétrie orthogonale. Préciser ses caractéristiques.
b) Montrer que f commute avec s si et seulement si u est un vecteur propre de f.
c) En déduire l’ensemble des endomorphismes orthogonaux commutant avec tous les éléments de
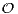 (E).
(E).
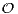 n(R) ∩
n(R) ∩ n(Z) ?
n(Z) ?
 N* tel que
Ak = In . Montrer que A2 = In.
N* tel que
Ak = In . Montrer que A2 = In.
 N * , Tp = T + diag(1⁄p,2⁄p,…,n⁄p).
N * , Tp = T + diag(1⁄p,2⁄p,…,n⁄p).
a) Montrer qu’à partir d’un certain rang, Tp a n valeurs propres distinctes.
b) En déduire que toute matrice de  n(C) est limite d’une suite de matrices diagonalisables.
n(C) est limite d’une suite de matrices diagonalisables.
 N*, un = 1 +
N*, un = 1 + 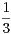 +
+  +
+ 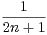 -αln(n). Donner une condition nécessaire
et suffisante sur α pour que (un) converge.
-αln(n). Donner une condition nécessaire
et suffisante sur α pour que (un) converge.
 N, un+1 = un + 1⁄un.
N, un+1 = un + 1⁄un.
a) Montrer que un diverge vers + ∞.
b) Montrer que 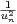 ≤
≤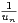 , en déduire que 2 ≤ u
, en déduire que 2 ≤ u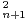 - u
- u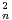 ≤ 2 + un+1 - un.
≤ 2 + un+1 - un.
c) Montrer que un ∽ 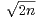 .
.
 N, l’existence et l’unicité d’un réel xn tel que xn - e-xn = n.
Montrer que xn
N, l’existence et l’unicité d’un réel xn tel que xn - e-xn = n.
Montrer que xn  [n,n + 1]. En déduire un équivalent de xn puis un développement asymptotique
à deux termes de xn, lorsque n → +∞.
[n,n + 1]. En déduire un équivalent de xn puis un développement asymptotique
à deux termes de xn, lorsque n → +∞.
 R2 pour que la série de terme général
R2 pour que la série de terme général
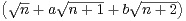 soit convergente.
soit convergente.
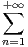 ln
ln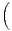 1 +
1 + 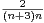
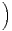 .
.
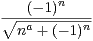 où a
où a  R+*.
R+*.
 R et, pour n
R et, pour n  N, un+1 =
N, un+1 = 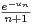 .
.
a) Déterminer la limite de (un) et de (nun).
b) Nature des séries de termes généraux un et (-1)nun ?
 N, un+1eun+1 =
N, un+1eun+1 = 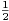 un.
un.
a) Montrer ces conditions définissent une unique suite (un).
b) Montrer que (un) converge et trouver sa limite.
c) Montrer que la série de terme général un converge.
d) l’aide de la série de terme général ln(2n+1un+1) - ln(2nun), montrer qu’il existe une
constante c > 0 telle que un ~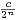 .
.
 ]0,1[ et, pour n ≥ 0, un+1 =
]0,1[ et, pour n ≥ 0, un+1 = 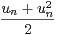 . Montrer que la série de terme
général un converge.
. Montrer que la série de terme
général un converge.

 1(R+, R+*). On suppose que fʹ(x)⁄f(x) tend vers l < 0 quand x tend
vers + ∞. Quelle est la nature de la série de terme général f(n) ?
1(R+, R+*). On suppose que fʹ(x)⁄f(x) tend vers l < 0 quand x tend
vers + ∞. Quelle est la nature de la série de terme général f(n) ?
b) Soit f 
 1 (R +, R+*). On suppose qu’il existe a > 0 tel que fʹ(x)⁄f(x) ∽ -a⁄x quand x tend
vers + ∞. Discuter selon a de la nature de la série de terme général f(n).
1 (R +, R+*). On suppose qu’il existe a > 0 tel que fʹ(x)⁄f(x) ∽ -a⁄x quand x tend
vers + ∞. Discuter selon a de la nature de la série de terme général f(n).
 ]0,π⁄2[ et, pour n
]0,π⁄2[ et, pour n  N, un+1 = sin(un).
N, un+1 = sin(un).
a) Établir la convergence de cette suite et déterminer sa limite.
b) En considérant un+1 - un montrer que 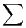 u
u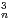 converge.
converge.
c) En considérant ln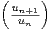 montrer que
montrer que 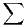 u
u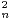 diverge.
diverge.
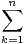
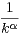 et Rn =
et Rn = 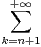
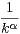 . tudier la convergence de la série
de terme général Rn⁄Sn.
. tudier la convergence de la série
de terme général Rn⁄Sn.
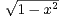 = π⁄2.
= π⁄2.
∀x  R +,
R +, 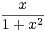 ≤ arctanx ≤ x.
≤ arctanx ≤ x.
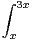
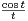 d t.
d t.
 x + ln(1 + x).
x + ln(1 + x).
a) Montrer que f définit une bijection de ] - 1,+∞[ sur un intervalle à préciser. Prouver que la
réciproque g de f est de classe  ∞.
∞.
b) Calculer g(0) et gʹ(0). Calculer le développement limité de g à l’ordre 3 en 0.
 R2 avec a < b et f
R2 avec a < b et f 
 0([a,b], R) telle que :
0([a,b], R) telle que :
∀x  [a, b], f(a + b - x) = f(x). Montrer que
[a, b], f(a + b - x) = f(x). Montrer que 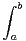 tf(t)d t =
tf(t)d t = 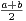
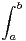 f(t)d t. Calculer
f(t)d t. Calculer
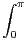
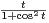 dt.
dt.
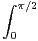 ln(sint)d t et J =
ln(sint)d t et J = 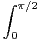 ln(cost)d t. Montrer que I et J sont
convergentes et que I = J. Calculer I + J, en déduire I et J.
ln(cost)d t. Montrer que I et J sont
convergentes et que I = J. Calculer I + J, en déduire I et J.
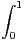 t
t 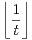 d t.
d t.
a) Trouver trois réels a, b et c tels que : ∀x  R+*,
R+*, 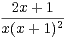 =
= 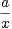 +
+ 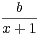 +
+ 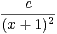 .
.
b) L’intégrale I converge-t-elle ?
c) Calculer I.
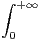
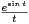 d t et J =
d t et J = 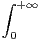 sintsin
sintsin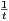 d t.
d t.
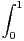 tn ln2td t, où n
tn ln2td t, où n  N.
N.
b) Convergence de l’intégrale 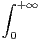
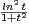 d t.
d t.
c) Montrer : 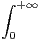
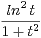 d t = 2
d t = 2 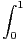
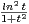 d t.
d t.
 e-x2
. On donne :
e-x2
. On donne : 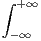 f(x)d x =
f(x)d x = 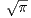 .
.
a) Montrer que l’on peut écrire f(n)(x) = f(x)Pn(x) où Pn est un polynôme. Préciser le degré et le coefficient dominant de Pn.
b) Existence puis calcul de 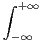 f(x)Pn(x)Pm(x)d x.
f(x)Pn(x)Pm(x)d x.
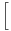
 1 +
1 + 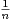
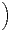 x
x![]](/numeros/RMS127-4/RMS127-4840x.png) .
.
 N, soit un : x
N, soit un : x
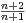 e-nx2
.
e-nx2
.
tudier la convergence simple de (un) sur R. Y a-t-il convergence uniforme sur [0,+∞[ ? sur [a, +∞[ pour a > 0 ?
 N*, on note Gn :
N*, on note Gn : ![({ [0,1] -→ R
( t)n
( t ↦→ 1 - -- et
n](/numeros/RMS127-4/RMS127-4843x.png) .
.
a) Montrer que : ∀n  N*, ∀t
N*, ∀t  [0,1], |Gʹn(t)|≤
[0,1], |Gʹn(t)|≤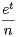 .
.
b) En déduire que : ∀n  N*, ∀t
N*, ∀t  [0,1],
[0,1], 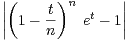 ≤
≤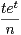 .
.
c) On définit , pour n  N* et x
N* et x  [0,1], In(x) =
[0,1], In(x) = 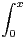
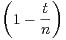 n et d t. Montrer que la suite de
fonctions (In ) converge simplement sur [0,1].
n et d t. Montrer que la suite de
fonctions (In ) converge simplement sur [0,1].
d) Converge-t-elle uniformément sur [0,1] ?

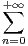 ln
ln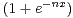 . Donner le domaine de définition D de F . La fonction
F est-elle continue sur D ? Déterminer F(D).
. Donner le domaine de définition D de F . La fonction
F est-elle continue sur D ? Déterminer F(D).
 N*,∀x
N*,∀x  [0,1],un(x) = ln
[0,1],un(x) = ln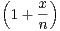 -
-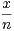 et S =
et S = 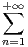 un.
un.
a) Montrer que S est de classe C1 sur [0,1].
b) Calculer Sʹ(1).
 N, un : x
N, un : x an
an 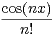 .
.
a) Étudier la convergence simple et la convergence uniforme de la série de fonctions
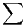 un.
un.
b) Calculer la somme S de cette série de fonctions.
c) Calculer pour p  N,
N, 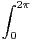 S(x)cos(px)d x et
S(x)cos(px)d x et 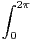 S(x)sin(px)d x
S(x)sin(px)d x
 N. En déduire une expression de
N. En déduire une expression de
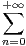
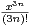 pour x
pour x  R.
R.

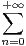
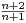 xn. Déterminer le rayon de convergence de S(x), puis donner une
expression de S avec des fonctions usuelles.
xn. Déterminer le rayon de convergence de S(x), puis donner une
expression de S avec des fonctions usuelles.
 N, an = 2(-1)n
.
N, an = 2(-1)n
.
a) Quel est le rayon de convergence de la série entière de terme général (anxn)n ?
b) Exprimer la somme de cette série entière sur son intervalle de définition à l’aide des fonctions usuelles.
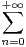 anxn a un rayon de convergence
infini.
anxn a un rayon de convergence
infini.
a) Quel est le rayon de convergence de la série entière g(x) = 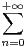 bnxn ?
bnxn ?
b) Montrer qu’il existe une suite (γn) tendant vers 0 telle que an = bn(1 + γn) pour tout
n  N .
N .
c) Soit p  N . Justifier l’existence de vp = supn≥p|γn|.
N . Justifier l’existence de vp = supn≥p|γn|.
d) Établir l’inégalité : ∀x > 0, 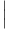
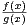 - 1
- 1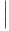 ≤
≤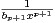
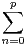 bn|γn|xn + vp+1.
bn|γn|xn + vp+1.
e) Montrer que f(x) ~ g(x) lorsque x → +∞.
f) Application. Trouver un équivalent au voisinage de + ∞ de 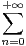
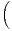 1 +
1 + 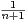
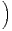 n+1
n+1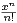 .
.
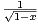 .
.
b) En déduire celui de 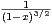 .
.
c) l’aide d’un produit de Cauchy, montrer que 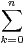
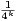
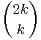 =
= 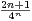
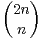 .
.
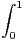
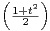 n d t.
n d t.
a) Montrer que la suite (an) est convergente, et déterminer sa limite.
b) Montrer que la série de terme général (-1)nan est convergente.
c) Montrer que : ∀n  N, an ≥ 1⁄(2n + 1). En déduire le rayon de convergence R de
N, an ≥ 1⁄(2n + 1). En déduire le rayon de convergence R de
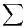 anxn.
anxn.
d) Soit f : x
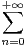 anxn. Montrer que f vérifie sur ] -R,R[ une équation différentielle que l’on
explicitera. Ind. Chercher une relation de récurrence entre les an.
anxn. Montrer que f vérifie sur ] -R,R[ une équation différentielle que l’on
explicitera. Ind. Chercher une relation de récurrence entre les an.
 R avec |a| < 1 et f : x
R avec |a| < 1 et f : x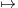
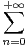 sin(anx).
sin(anx).
a) Montrer que f est définie et de classe C∞ sur R.
b) Montrer que, pour tout k  N*, |fk(x)|≤
N*, |fk(x)|≤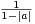 .
.
c) Montrer que f est développable en série entière sur R.
 N, on pose In =
N, on pose In = 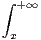
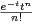 d t. Justifier l’existence de In puis
déterminer la limite de la suite (In).
d t. Justifier l’existence de In puis
déterminer la limite de la suite (In).
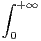
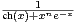 d x.
d x.
 N, In =
N, In = 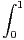
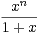 d x.
d x.
a) Montrer que limn→+∞In = 0.
b) Calculer I0 , I1, In + In+1.
c) Montrer que : ∀n  N*, (-1)n In = ln2 +
N*, (-1)n In = ln2 + 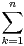
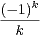 .
.
d) Montrer que la série de terme général 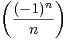 n≥1 converge et calculer sa somme.
n≥1 converge et calculer sa somme.
 N, on pose Ip =
N, on pose Ip = 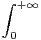
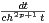 .
.
a) Justifier l’existence de Ip.
b) Calculer I0 .
c) Trouver une relation entre Ip et Ip+1.
d) Calculer Ip .
 N, soit In(α) =
N, soit In(α) = 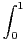 tn(1 - t)α d t.
tn(1 - t)α d t.
a) Pour quelles valeurs de α cette suite est-elle définie ? convergente ?
b) Pour quelles valeurs de α la série de terme général In(α) est-elle convergente ? Calculer alors la somme de la série.
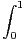
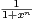 d x lorsque
n → +∞.
d x lorsque
n → +∞.
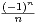
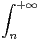 e-t2
d t et
e-t2
d t et
(-1)n 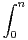 e-n2t2
d t.
e-n2t2
d t.
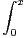
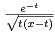 d t. Déterminer la limite de f
en + ∞.
d t. Déterminer la limite de f
en + ∞.

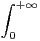
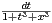 .
.
a) Montrez que f est définie et continue sur R+.
b) Calculez f(0). Ind. On pourra poser u = 1⁄t.
c) Déterminer la limite de f(x) quand x tend vers + ∞.
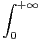
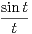 d t et F(x) =
d t et F(x) = 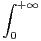
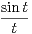
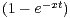 d t
d t
a) Montrer que I est bien définie.
b) Montrer que F est définie sur [0,+∞[, que F est continue sur [0,+∞[ et que F est dérivable sur ]0, +∞[.
c) En déduire la valeur de I.
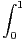
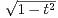 cos(xt)d t. Montrer que f est paire et de classe
cos(xt)d t. Montrer que f est paire et de classe  2 sur
R. Montrer que f est solution de l’équation xyʹʹ + 3yʹ + xy = 0. Ind. Utiliser une intégration par
parties.
2 sur
R. Montrer que f est solution de l’équation xyʹʹ + 3yʹ + xy = 0. Ind. Utiliser une intégration par
parties.
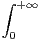 e-x2
cos(2xt)d x.
e-x2
cos(2xt)d x.
a) Montrer que f est définie et continue sur R.
b) Montrer que f est de classe  1 sur R et calculer fʹ.
1 sur R et calculer fʹ.
c) On admet que 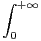 e-x2
d x =
e-x2
d x = 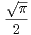 . Exprimer f à l’aide des fonctions usuelles.
. Exprimer f à l’aide des fonctions usuelles.
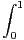 ln(t) ln(1 - tx)d t.
ln(t) ln(1 - tx)d t.
a) Montrer que I est définie sur R+*.
b) Montrer que I est une fonction croissante.
c) Calculer , pour tout a > 0, 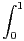 ta ln(t)d t
ta ln(t)d t
d) En déduire une expression de I comme somme de série.
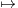
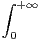
 d t.
d t.
a) Quel est le domaine de définition de f ? Calculer f(0).
b) Étudier la continuité de f.
c) Montrer que f est de classe  2 sur R+* et trouver une équation différentielle vérifiée par
f.
2 sur R+* et trouver une équation différentielle vérifiée par
f.
d) Quelle est la limite de f en + ∞ ?

 0([0,1], R) et G : x
0([0,1], R) et G : x  [0,1]
[0,1]
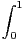 |x - t|g(t)d t.
|x - t|g(t)d t.
a) Montrer que G est de classe  2 et calculer Gʹʹ.
2 et calculer Gʹʹ.
b) En déduire l’existence d’une fonction f telle que fʹʹ = g et f(0) = f(1) = 0. Y a-t-il unicité d’une telle fonction f ?
 N, on pose un =
N, on pose un = 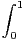 xn sin(πx)d x.
xn sin(πx)d x.
a) Montrer que la série de terme général un converge.
b) Montrer que 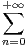 un =
un = 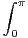
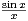 d x.
d x.
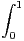
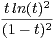 dt
dt
a) Justifier l’existence de I.
b) Montrer que I = 2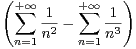 .
.
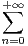 (-1)n
(-1)n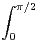 cosnxd x et calcul de la somme.
cosnxd x et calcul de la somme.
 N, soit fn : t
N, soit fn : t  [0,1]
[0,1]
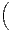
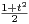
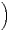 n.
n.
a) Montrer que la suite (fn) converge simplement.
b) Montrer que la suite (an) définie par an = 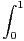 fn converge.
fn converge.
c) Montrer que la série 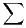 (-1)nan converge et calculer sa somme.
(-1)nan converge et calculer sa somme.
a) Montrer que si y1 et y2 sont solutions de (E) alors yʹ1y2 - yʹ2y1 est constante sur R.
b) Montrer que si y est une solution de (E) bornée sur R alors yʹ(x) admet une limite finie quand x tend vers + ∞, puis montrer que cette limite est forcément nulle.
c) Montrer que (E) admet nécessairement une solution non bornée.
 R+* et E l’équation différentielle xyʹ + λy =
R+* et E l’équation différentielle xyʹ + λy = 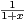 .
.
a) Exprimer à l’aide d’une intégrale les solutions de E sur R+*.
b) Montrer qu’il existe une unique solution bornée au voisinage de 0+.
a) Déterminer les fonctions développables en série entière solutions de (*). Pourquoi y a-t-il d’autres solutions ?
b) Déterminer toutes les solutions de (*) sur R. On fera le changement de variable y(x) = z(x)⁄(1 - x) et on soignera les raccords.
 .
.
a) Justifier sans calcul que A est diagonalisable.
b) Déterminer les valeurs propres et une base de vecteurs propres de A.
c) Résoudre le système différentiel 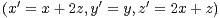 .
.
 x2 + xy + y2 - 5x-y.
x2 + xy + y2 - 5x-y.
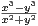 pour (x,y)≠(0,0) et f(0,0) = 0. La fonction f est-elle continue
sur R 2 ?
pour (x,y)≠(0,0) et f(0,0) = 0. La fonction f est-elle continue
sur R 2 ?  1 sur R 2 ? Existence et calcul de
1 sur R 2 ? Existence et calcul de 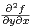 .
.
 [-1,1]2
[-1,1]2 y3x4 + ln(1 + y4). Cette fonction admet-elle des extrema
globaux ? locaux ?
y3x4 + ln(1 + y4). Cette fonction admet-elle des extrema
globaux ? locaux ?
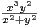 si (x,y)
si (x,y)  R2 \{(0,0)} et f(0,0) = 0. Montrer que la fonction f
ainsi définie est de classe
R2 \{(0,0)} et f(0,0) = 0. Montrer que la fonction f
ainsi définie est de classe  1 sur R2.
1 sur R2.
a) Montrer qu’il existe une base orthonormale (e1,e2,...,en) telle que f soit représenté dans cette base par une matrice diagonale.
b) Montrer que, pour tout x  E \{0}, ⟨f(x),x⟩ > 0.
E \{0}, ⟨f(x),x⟩ > 0.
c) On suppose dorénavant que E = Rn, muni du produit scalaire canonique. Soit v  Rn. Pour tout
x
Rn. Pour tout
x  R n , on note g(x) =
R n , on note g(x) = 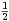 ⟨f(x),x⟩-⟨v,x⟩. Montrer que g est de classe
⟨f(x),x⟩-⟨v,x⟩. Montrer que g est de classe  1 et que pour x,h
1 et que pour x,h  E,
on a dgx (h) = limt→0
E,
on a dgx (h) = limt→0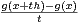 .
.
d) En déduire la valeur de la différentielle de g en x appliquée aux ei et la valeur du gradient de g.
e) Montrer que g n’admet qu’un seul point critique c que l’on précisera.
f) Montrer que g atteint au point c un minimum global. Y a-t-il d’autres extrema ?
a) Soient n, p  N. Montrer que la probabilité qu’aucun des événements An,...,An+p ne se réalise
est inférieure ou égale à exp
N. Montrer que la probabilité qu’aucun des événements An,...,An+p ne se réalise
est inférieure ou égale à exp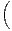 -
-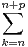 P(Ak)
P(Ak)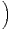 .
.
b) On suppose que la série de terme général P(An) est divergente. Montrer qu’il est presque impossible qu’il n’y ait qu’un nombre fini d’entiers n pour lesquels An est réalisé.
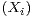 0≤i≤k suivant une même loi à valeurs dans N. On suppose que toutes
ces variables aléatoires sont mutuellement indépendantes. On définit enfin une variable
aléatoire Y par Y (ω) =
0≤i≤k suivant une même loi à valeurs dans N. On suppose que toutes
ces variables aléatoires sont mutuellement indépendantes. On définit enfin une variable
aléatoire Y par Y (ω) = 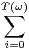 Xi(ω). Montrer que si les Xi admettent une espérance alors Y
aussi. Donner sous ces hypothèses une expression de E(Y ) en fonction de E(Xi) et
E(T).
Xi(ω). Montrer que si les Xi admettent une espérance alors Y
aussi. Donner sous ces hypothèses une expression de E(Y ) en fonction de E(Xi) et
E(T).
 N*, P(N = n) =
N*, P(N = n) = 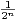 . Le joueur gagne N jetons si N est pair ; il perd N jetons
si N est impair.
. Le joueur gagne N jetons si N est pair ; il perd N jetons
si N est impair.
a) Quelle est la probabilité de gagner une partie ?
b) Déterminer la loi et l’espérance de la variable aléatoire G égale au gain algébrique du joueur.
a) Justifier que Xn est bien une variable aléatoire discrète et donner sa loi.
b) Justifier l’existence de l’espérance de Xn et la calculer.
c) On note Y n le rang du premier tirage à l’issue duquel toutes les boules ont été tirées au moins une fois. Donner la loi de Y 2 puis celle de Y 3.
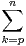
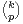 =
= 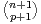 . On dispose d’une urne contenant
n boules numérotées de 1 à n. On tire deux boules au hasard. On note X (resp. Y ) la
variable aléatoire correspondant au numéro le plus petit (resp. le plus grand) des deux
boules.
. On dispose d’une urne contenant
n boules numérotées de 1 à n. On tire deux boules au hasard. On note X (resp. Y ) la
variable aléatoire correspondant au numéro le plus petit (resp. le plus grand) des deux
boules.
a) Déterminer la loi de (X,Y ). En déduire les lois de X et de Y .
b) Calculer E(Y ), E(Y (Y - 2)) et V (Y ).
c) Montrer que n + 1 - X suit la même loi que Y . Calculer E(X) et V (X).
d) Calculer E(X(Y - 2)) et Cov(X,Y ).
a) Déterminer la loi de Xk et la fonction de répartition F associée à Xk.
b) On note Zn la valeur maximale obtenue au bout de n lancers. Déterminer la fonction de répartition Fn de Zn en fonction de F .
c) Déterminer la limite de (Fn) lorsque n tend vers l’infini. La convergence est-elle uniforme ?
d) On note Y n la valeur minimale obtenue au bout de n lancers. Déterminer sa fonction de répartition.
 ]0,1[. On note N et S les variables aléatoires qui comptent respectivement le
nombre de particules arrivant sur le capteur et le nombre de particules détectées. On suppose que N
suit une loi de Poisson de paramètre λ.
]0,1[. On note N et S les variables aléatoires qui comptent respectivement le
nombre de particules arrivant sur le capteur et le nombre de particules détectées. On suppose que N
suit une loi de Poisson de paramètre λ.
a) Soient s, n  N. Calculer P(S = s∣N = n) et P(S = s et N = n). En déduire la loi de
S.
N. Calculer P(S = s∣N = n) et P(S = s et N = n). En déduire la loi de
S.
b) Donner la loi de N - S sans calcul.
c) Les variables S et N - S sont-elles indépendantes ?
d) Même question pour S et N.
a) Calculer P(Y = 0). Soit n  N. Montrer que P(X1 - X2 = n) =
N. Montrer que P(X1 - X2 = n) = 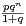 . En déduire la loi de
Y .
. En déduire la loi de
Y .
b) Montrer que Y admet une espérance et la calculer.
c) Montrer que E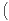 (X1 - X2)2
(X1 - X2)2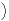 = 2V (X1). En déduire que Y admet une variance et la
calculer.
= 2V (X1). En déduire que Y admet une variance et la
calculer.
 N* une suite de variables aléatoires mutuellement indépendantes suivant toutes
une loi de Bernoulli de paramètre p
N* une suite de variables aléatoires mutuellement indépendantes suivant toutes
une loi de Bernoulli de paramètre p  ]0,1[. On note ∀n
]0,1[. On note ∀n  N*, Y n = Xn + Xn+1 et
Mn =
N*, Y n = Xn + Xn+1 et
Mn = 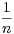
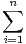 Y i
Y i
a) Les variables aléatoires Y n sont-elles mutuellement indépendantes ?
b) Calculer l’espérance et la variance de Mn.
c) Énoncer la loi faible des grands nombres. Peut-on l’appliquer ici ?
 R+* et qu’il existe p
R+* et qu’il existe p  [0,1] tel que, pour tout m
[0,1] tel que, pour tout m  N, la loi
conditionnelle de X sachant Y = m est la loi binomiale de paramètres (m,p). Donner la loi de
X.
N, la loi
conditionnelle de X sachant Y = m est la loi binomiale de paramètres (m,p). Donner la loi de
X.
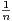
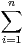 pi
pi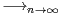 p. Montrer que, ∀ε > 0,
P
p. Montrer que, ∀ε > 0,
P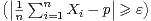
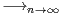 0.
0.
 N*. On considère N = an clients qui s’approvisionnent chez n
fournisseurs. Chaque client choisit un fournisseur au hasard. Pour i
N*. On considère N = an clients qui s’approvisionnent chez n
fournisseurs. Chaque client choisit un fournisseur au hasard. Pour i  [[1,n]], on note
Xi le nombre de clients du fournisseur i et Y le nombre de fournisseurs n’ayant aucun
client.
[[1,n]], on note
Xi le nombre de clients du fournisseur i et Y le nombre de fournisseurs n’ayant aucun
client.
a) Donner la loi, l’espérance et la variance de Xi.
b) Que vaut X1 +  + Xn ? En déduire E(XiXj) et Cov(Xi,Xj) pour i≠j. Donner
l’expression du coefficient de corrélation linéaire de Xi et Xj.
+ Xn ? En déduire E(XiXj) et Cov(Xi,Xj) pour i≠j. Donner
l’expression du coefficient de corrélation linéaire de Xi et Xj.
c) Soit βi la variable aléatoire indicatrice de l’événement : ≪ le fournisseur i n’a pas de client ≫. Exprimer Y en fonction des βi. Déterminer E(Y ).
d) Calculer Cov (βi,βj).
e) Déterminer la variance de Y .
 la courbe d’équation :
la courbe d’équation : 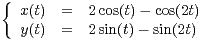 . Tracer cette courbe en
précisant les tangentes éventuelles.
. Tracer cette courbe en
précisant les tangentes éventuelles.
b) Écrire une fonction jours(j,m,a) qui comptabilise le nombre de jours écoulés entre le 1er janvier de l’année a et la date j/m/a saisie en argument.
b) Écrire une fonction nombreDeJours(j,m,a) qui renvoie le nombre de jours écoulés entre le 1er janvier 1970 et la date j/m/a.
d) Les horloges internes des ordinateurs étaient autrefois codées sur 32 bits, soit un décompte de 232 - 1 secondes au maximum. Les horloges sont initialisées au 1er janvier 1970. quelle date un bug se produira-t-il ?
b) crire une fonction somme qui à tout entier naturel associe la somme de ses chiffres.
c) Un nombre est dit adéquat si la somme de ses chiffres est un multiple de 10. Écrire une fonction test qui renvoie le booléen True si le nombre est adéquat, et False sinon.
d) Écrire une fonction modification(n) qui change le chiffre des unités de n pour qu’il soit adéquat. Si n est déjà adéquat, la fonction le renvoie sans modification.
e) Tester la fonction pour dix entiers choisis au hasard entre 10000 et 100000 grâce à la fonction randint.
b) crire une fonction qui prend en arguments p, q et un entier n et qui renvoie une liste contenant les n premières décimales de p⁄q.
c) La partie décimale de certains nombres est périodique à partir d’un certain rang (par exemple 12,72123123123...). crire une fonction d’arguments p et q, qui renvoie la partie périodique de p⁄q.
d) Soit e un nombre décimal dont la partie décimale est périodique à partir d’un certain rang. crire une fonction qui renvoie deux entiers p et q premiers entre eux tels que p⁄q = e.
>> from numpy.random import rand
>> LR = rand(6)
>> LR<0.5
>> 1*(LR<0.5)
b) Créer une fonction tirer qui prend en argument un entier n et renvoie une liste de n tirages successifs indépendants suivant la loi de Bernoulli de paramètre 1⁄2.
c) Calculer numériquement l’espérance du nombre de tirages ayant donné un 1.
d) Créer une fonction qui prend en argument une liste seq de 0 et de 1 et renvoie le temps d’apparition de la séquence seq, c’est-à-dire le nombre de tirages à faire pour trouver cette séquence dans la liste des tirages. Par exemple, pour la séquence [1,0,1,1] dans la liste [0,0,1,0,0,1,0,1,1], la fonction renvoie 8.
[Épreuves orales des concours]

