[Épreuves orales des concours]Algèbre
a) Montrer que P a trois racines simples a, b et c.
b) Calculer a2 + b2 + c2 et a7 + b7 + c7.
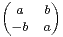 , avec a et b réels.
, avec a et b réels.
a) Montrer que E est un sous-espace vectoriel de  2(R) et donner sa dimension.
2(R) et donner sa dimension.
b) Montrer que E est un sous-anneau de  2(R).
2(R).

 n(C) et ϕA l’application définie de
n(C) et ϕA l’application définie de  n(C) dans lui-même
par ϕA (M) = AM. Trouver une condition nécessaire et suffisante pour que ϕA soit
bijective.
n(C) dans lui-même
par ϕA (M) = AM. Trouver une condition nécessaire et suffisante pour que ϕA soit
bijective.
 N*, A
N*, A 
 n(R) et ϕ une forme linéaire de
n(R) et ϕ une forme linéaire de  n(R). Trouver une condition
nécessaire et suffisante sur ϕ(A) pour que l’application f : M
n(R). Trouver une condition
nécessaire et suffisante sur ϕ(A) pour que l’application f : M M - ϕ(M)A soit bijective de
M - ϕ(M)A soit bijective de
 n (R ) sur lui-même.
n (R ) sur lui-même.
 n(R). Montrer l’existence d’une matrice A
n(R). Montrer l’existence d’une matrice A 
 n(R)
telle que ∀M
n(R)
telle que ∀M 
 n(R), ϕ(M) = Tr(AM).
n(R), ϕ(M) = Tr(AM).

 (E). On
définit ϕ sur E3 par ϕ(x,y,z) = dete(u(x),y,z) + dete(x,u(y),z) + dete(x,y,u(z)). Étudier
ϕ.
(E). On
définit ϕ sur E3 par ϕ(x,y,z) = dete(u(x),y,z) + dete(x,u(y),z) + dete(x,y,u(z)). Étudier
ϕ.
 N*,d
N*,d![[k]
i](/numeros/RMS127-4/RMS127-4562x.png) = di(di - 1)
= di(di - 1) (di - k + 1) et d
(di - k + 1) et d![[0]
i](/numeros/RMS127-4/RMS127-4564x.png) = 1. Calculer
V (d1 , ..., dn ) =
= 1. Calculer
V (d1 , ..., dn ) = ![|| ||
|| 1 1 ... 1 ||
|| d1 d2 ... dn ||
||[..n.-1] [n..-.1] ... [..n-.1]||
d1 d2 ... dn](/numeros/RMS127-4/RMS127-4565x.png)
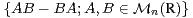 .
.
a) Montrer que l’application trace Tr est une forme linéaire sur  n(R), et que Tr(AB) = Tr(BA)
pour tout couple de matrices.
n(R), et que Tr(AB) = Tr(BA)
pour tout couple de matrices.
b) On note (Ei,j )1≤i,j≤n la base canonique de  n(R). Calculer Ei,jEi,i et Ei,iEi,j si
i ⁄= j.
n(R). Calculer Ei,jEi,i et Ei,iEi,j si
i ⁄= j.
c) Soit ϕ une forme linéaire de  n(R) telle que, pour tout couple (A,B) de matrices,
ϕ(AB) = ϕ(BA). Montrer que la famille (ϕ, Tr) est liée.
n(R) telle que, pour tout couple (A,B) de matrices,
ϕ(AB) = ϕ(BA). Montrer que la famille (ϕ, Tr) est liée.
d) Montrer que H = Ker(Tr).
e) Trouver un supplémentaire de H.


 n (R ), à coefficients non nuls.
n (R ), à coefficients non nuls.
a) Quel est le rang de la matrice A ?
b) Donner une condition nécessaire et suffisante pour que A soit la matrice d’un projecteur.
c) On revient au cas général. On pose B = 2A - Tr(A)In.
d) Calculer le déterminant de B.
e) Donner une condition nécessaire et suffisante pour que B soit inversible.
f) Calculer B2 . Calculer B-1 dans le cas où B est inversible.
 (E)
tels que Im (f + g) = Im(f) ⊕ Im(g). Montrer E = Ker(f) + Ker(g).
(E)
tels que Im (f + g) = Im(f) ⊕ Im(g). Montrer E = Ker(f) + Ker(g).

 (E) vérifiant f3 = id.
(E) vérifiant f3 = id.
a) Montrer que E = Ker(f - id) ⊕ Im(f - id).
b) Montrer que Ker(f - id) = Im(f2 + f + id).
c) Montrer que Ker(f2 + f + id) = Im(f - id).

 n(C) telles que rg(AB - BA) = 1. Déterminer (AB - BA)2.
n(C) telles que rg(AB - BA) = 1. Déterminer (AB - BA)2.
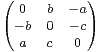 .
Calculer etA pour t
.
Calculer etA pour t  R.
R.
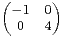 .
Déterminer les M
.
Déterminer les M 
 2(
2( ) vérifiant M3 - 2M = D.
) vérifiant M3 - 2M = D.
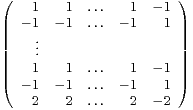

 2n+1 (R ). Montrer que M est diagonalisable et la diagonaliser explicitement.
2n+1 (R ). Montrer que M est diagonalisable et la diagonaliser explicitement.
 N*, Jn
N*, Jn 
 n(R) la matrice dont tous les coefficients sont nuls, sauf ceux
d’indice de la forme (i,n + 1 - i) qui valent 1 et An =
n(R) la matrice dont tous les coefficients sont nuls, sauf ceux
d’indice de la forme (i,n + 1 - i) qui valent 1 et An =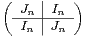 Diagonaliser Jn . La matrice An est-elle diagonalisable ?
Diagonaliser Jn . La matrice An est-elle diagonalisable ?

 n(R), B =
n(R), B = 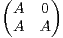 , P un polynôme de
, P un polynôme de  [X].
[X].
a) Calculer P(B).
b) Donner une condition nécessaire et suffisante pour que B soit diagonalisable.
 n(C). On note FA l’endomorphisme de
n(C). On note FA l’endomorphisme de  n(C) qui à une
matrice M associe FA(M) = AM. Comparer les spectres de A et de FA.
n(C) qui à une
matrice M associe FA(M) = AM. Comparer les spectres de A et de FA.

 (E) et μ le polynôme minimal
de u. Soit P
(E) et μ le polynôme minimal
de u. Soit P  C [X]. Montrer que P(u) est dans GL(E) si et seulement si μ et P sont premiers
entre eux.
C [X]. Montrer que P(u) est dans GL(E) si et seulement si μ et P sont premiers
entre eux.
 n(C) qui n’est pas diagonalisable.
n(C) qui n’est pas diagonalisable.
b) L’ensemble des matrices diagonalisables de  n(C) est-il un sous-espace vectoriel ?
n(C) est-il un sous-espace vectoriel ?

 (E) diagonalisable, χu son
polynôme caractéristique, (e1,…,en) une base de vecteurs propres de u.
(E) diagonalisable, χu son
polynôme caractéristique, (e1,…,en) une base de vecteurs propres de u.
a) Montrer que χu(u) = 0 sans utiliser le théorème de Cayley-Hamilton.
b) Soit x = 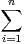 xiei un élément de E. Calculer dete(x,u(x),…,un-1(x)).
xiei un élément de E. Calculer dete(x,u(x),…,un-1(x)).
c) Montrer que les valeurs propres de u sont simples si et seulement si on peut trouver x  E tel
que (x, u(x), … , un-1(x)) soit une base de E.
E tel
que (x, u(x), … , un-1(x)) soit une base de E.

 (E) un
endomorphisme ayant n valeurs propres distinctes.
(E) un
endomorphisme ayant n valeurs propres distinctes.
a) Que peut-on dire de u ?
b) Montrer que si g 
 (E) est solution de l’équation (E) g2 = u, alors tout vecteur propre de u
est aussi vecteur propre de g.
(E) est solution de l’équation (E) g2 = u, alors tout vecteur propre de u
est aussi vecteur propre de g.
c) Combien l’équation (E) admet-elle de solutions ?
 R[X], montrer que l’intégrale
R[X], montrer que l’intégrale 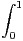
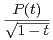 d t converge.
d t converge.
b) Soit E = R n [X]. Pour P,Q  E, on pose
E, on pose 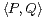 =
= 
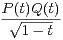 d t. Montrer que cette
application est un produit scalaire de E.
d t. Montrer que cette
application est un produit scalaire de E.
c) Soit A  E. On considère l’application fA qui à P
E. On considère l’application fA qui à P  E associe le reste de la division
euclidienne de P par A. Montrer que fA est un projecteur de E. Déterminer son image et son
noyau.
E associe le reste de la division
euclidienne de P par A. Montrer que fA est un projecteur de E. Déterminer son image et son
noyau.
 2([0,1], R). Pour f,g
2([0,1], R). Pour f,g  E, on pose
E, on pose 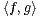 =
= 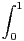 (fg + fʹgʹ).
(fg + fʹgʹ).
a) Montrer que  est un produit scalaire sur E.
est un produit scalaire sur E.
b) On note U l’ensemble des f  E vérifiant f(0) = f(1) = 0, et V l’ensemble des f
E vérifiant f(0) = f(1) = 0, et V l’ensemble des f  E
vérifiant fʹʹ = f. Montrer que U et V sont deux sous-espaces vectoriels de E, orthogonaux pour le
produit scalaire précédent.
E
vérifiant fʹʹ = f. Montrer que U et V sont deux sous-espaces vectoriels de E, orthogonaux pour le
produit scalaire précédent.
c) A-t-on U ⊕ V = E ?
 n(R) en posant, pour A et B dans
n(R) en posant, pour A et B dans
 n (R ),
n (R ), 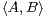 = Tr(tAB).
= Tr(tAB).
b) Soit M =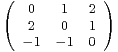 . Calculer la distance de M à
. Calculer la distance de M à  3(R).
3(R).
c) Soit H l’ensemble des matrices de  3(R) de trace nulle. Montrer que H est un sous-espace
vectoriel et calculer sa dimension. Soit J
3(R) de trace nulle. Montrer que H est un sous-espace
vectoriel et calculer sa dimension. Soit J 
 3(R) la matrice dont tous les coefficients sont égaux
à 1. Calculer la distance de J à H.
3(R) la matrice dont tous les coefficients sont égaux
à 1. Calculer la distance de J à H.
 ) un espace euclidien, a,b deux vecteurs unitaires indépendants, et
u : x
) un espace euclidien, a,b deux vecteurs unitaires indépendants, et
u : x  E
E
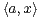 b +
b + 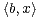 a.
a.
a) Montrer que u est un endomorphisme symétrique.
b) Trouver le noyau de u.
c) Trouver les valeurs propres et vecteurs propres de u.
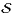 n(R),
λ1 ≤
n(R),
λ1 ≤  ≤ λn les valeurs propres de A comptées avec multiplicité. Pour X dans Rn, soit
qA (X) = t XAX.
≤ λn les valeurs propres de A comptées avec multiplicité. Pour X dans Rn, soit
qA (X) = t XAX.
a) Montrer, pour x dans Rn : λ1∥X∥2 ≤ qA(X) ≤ λn∥X∥2.
b) Donner une condition nécessaire et suffisante pour que q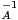 ({1}) soit un compact non vide de
Rn.
({1}) soit un compact non vide de
Rn.
 1 de [0,1] dans R. Pour f
1 de [0,1] dans R. Pour f  E, on
note N(f) =
E, on
note N(f) = 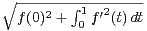 .
.
a) Montrer que N est une norme sur E.
b) La comparer à la norme ∥∥∞.
 (R) est un ouvert dense de
(R) est un ouvert dense de 
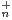 (R).
(R).
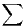 vn sont de même nature.
vn sont de même nature.
b) Pour tout n  N*, on pose xn =
N*, on pose xn = 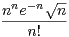 , puis yn = ln
, puis yn = ln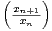 . Montrer que la série de
terme général yn converge.
. Montrer que la série de
terme général yn converge.
c) Montrer qu’il existe une constante c > 0 telle que limn→+∞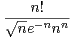 = c.
= c.
 R et, pour n
R et, pour n  N*,
N*,
vn = 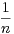
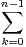 uk. Montrer que (vn) converge vers l.
uk. Montrer que (vn) converge vers l.
b) On considère la suite (un) définie par u0 = 1 et, pour n  N, un+1 = une-un.
N, un+1 = une-un.
c) Montrer que la suite (un) converge et donner sa limite.
d) On définit vn = 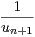 -
-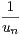 . Montrer que (vn) converge vers 1.
. Montrer que (vn) converge vers 1.
e) En déduire un équivalent de un. La série de terme général un converge-t-elle ?
 N, de classe
N, de classe  1. On suppose que f est d’intégrale
convergente sur [n0,+∞[, et que fʹ est intégrable sur cet intervalle. Montrer que la série
1. On suppose que f est d’intégrale
convergente sur [n0,+∞[, et que fʹ est intégrable sur cet intervalle. Montrer que la série 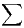 f(n)
converge. Montrer que
f(n)
converge. Montrer que 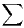
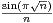 converge.
converge.

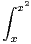 ln(t)2 d t.
ln(t)2 d t.
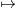 xα ln(1 + xβ).
xα ln(1 + xβ).
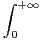
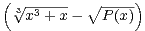 d x converge ?
d x converge ?
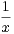
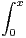 f(t)d t
f(t)d t
a) Peut-on prolonger g par continuité en 0 ? Si oui, avec quelle valeur de g(0) ?
b) Soit (a, b)  R2 avec 0 < a < b. Montrer
R2 avec 0 < a < b. Montrer  bg(t)2 d t = ag(a)2 - bg(b)2 + 2
bg(t)2 d t = ag(a)2 - bg(b)2 + 2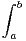 f(t)g(t)d t.
f(t)g(t)d t.
c) En déduire l’inégalité 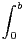 g(t)2 d t ≤ 4
g(t)2 d t ≤ 4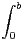 f(t)2 d t.
f(t)2 d t.
d) La fonction g2 est-elle intégrable sur [0,+∞[ ?
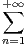
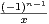 ln
ln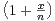
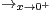 ln(2).
ln(2).
 N, un : x
N, un : x  R+*
R+*
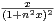 . Étudier la convergence simple et la
convergence uniforme sur R+* des séries de fonctions
. Étudier la convergence simple et la
convergence uniforme sur R+* des séries de fonctions 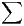 un et
un et 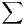 uʹn.
uʹn.
 [0,1] : 0 ≤ ln(1 + t⁄2) ≤ t⁄2 et - tln2 ≤ ln(1 - t⁄2) ≤ 0.
[0,1] : 0 ≤ ln(1 + t⁄2) ≤ t⁄2 et - tln2 ≤ ln(1 - t⁄2) ≤ 0.
b) On définit une suite de fonctions (fn) sur ] - 1,1[ par f0 : x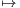 x et, pour n
x et, pour n  N,
fn+1 : x
N,
fn+1 : x ln
ln 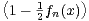 . Montrer que cette suite est bien définie et étudier la convergence de
la série
. Montrer que cette suite est bien définie et étudier la convergence de
la série 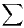 fn.
fn.
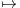
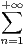
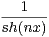 .
.
a) Déterminer le domaine de définition de f. Étudier la continuité de f.
b) Trouver la limite puis un équivalent de f(x) quand x → +∞.
c) Trouver la limite de f en 0.
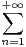
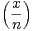 nx.
nx.

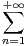
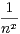 .
.
a) Quel est le domaine de définition de ζ ?
b) Montrer que ζ est continue sur ]1,+∞[.
c) Montrer que ζ est de classe  1, puis de classe
1, puis de classe  ∞.
∞.
d) Étudier la convexité de ζ.
b) Montrer que π = 8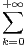
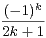 (
(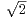 - 1)2k+1.
- 1)2k+1.
 N,
an+1 = -an - 2bn et bn+1 = an + 3bn.
N,
an+1 = -an - 2bn et bn+1 = an + 3bn.
a) Déterminer les rayons de convergence des deux séries entières de termes généraux 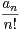 xn et
xn et
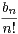 xn .
xn .
b) Calculer 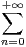
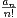 xn et
xn et 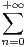
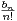 xn lorsque cela a un sens.
xn lorsque cela a un sens.

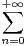 anzn une série entière de rayon de convergence infini.
anzn une série entière de rayon de convergence infini.
a) Soient r  R + et p
R + et p  N. Montrer
N. Montrer 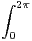 f(reit)e-ipt d t = 2πaprp.
f(reit)e-ipt d t = 2πaprp.
b) Montrer que si f est bornée alors f est constante.
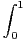 ln(x)ln(1 - xn)d x.
ln(x)ln(1 - xn)d x.
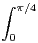 tanntd t.
tanntd t.
a) Montrer la convergence de la suite et déterminer sa limite. Déterminer la nature de la série de terme général (-1)nun.
b) Montrer que un+2 = 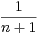 - un. Montrer que un est équivalente en l’infini à
- un. Montrer que un est équivalente en l’infini à 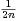 .
.
 N, on pose an =
N, on pose an = 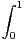
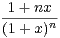 d x. Étudier la convergence de la suite (an)
de deux façons différentes.
d x. Étudier la convergence de la suite (an)
de deux façons différentes.
 N, An =
N, An = 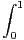
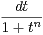
a) Déterminer la limite A de (An) quand n tend vers + ∞.
b) Déterminer un équivalent de A - An quand n tend vers + ∞.
c) Déterminer le rayon de convergence de la série entière  ln(An)zn.
ln(An)zn.
 R
R
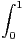
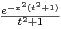 d t et F : x
d t et F : x  R
R
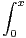 e-u2
d u. Exprimer G(x) en
fonction de F(x). En déduire la valeur de
e-u2
d u. Exprimer G(x) en
fonction de F(x). En déduire la valeur de 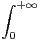 e-u2
d u.
e-u2
d u.
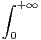
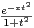 d t.
d t.
a) Montrer que G est continue sur  + et de classe
+ et de classe  1 sur
1 sur  +*.
+*.
b) Déterminer la limite de G en + ∞.
c) Montrer que G(x) - Gʹ(x) = 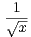
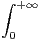 e-t2
d t et en déduire la valeur de
e-t2
d t et en déduire la valeur de 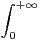 e-t2
d t.
e-t2
d t.

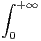
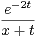 d t.
d t.
a) Étudier l’existence et la continuité de F sur R+*.
b) Déterminer la limite éventuelle de xF(x) quand x → +∞.
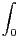 π⁄2
π⁄2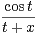 d t.
d t.
a) Montrer que F est bien définie et continue.
b) On pose G(x) =  π⁄2
π⁄2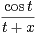 d t -
d t -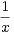
 π⁄2 costd t. Montrer que G(x) = O(1⁄x2) quand
x → +∞. En déduire un équivalent de F(x) quand x tend vers + ∞.
π⁄2 costd t. Montrer que G(x) = O(1⁄x2) quand
x → +∞. En déduire un équivalent de F(x) quand x tend vers + ∞.
c) Donner un équivalent de F en 0+.
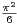 . Calculer
. Calculer 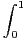
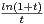 d t.
d t.
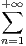
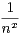
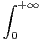 tx-1e-t d t =
tx-1e-t d t = 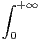
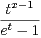 d t.
d t.
 R+
R+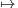
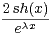 .
.
a) Montrer que fλ est bornée.
b) On suppose λ > 1. Montrer que fλ est intégrable et exprimer 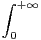 fλ(x)d x comme somme de
série.
fλ(x)d x comme somme de
série.
 et ln(t) est intégrable sur ]0,1[.
et ln(t) est intégrable sur ]0,1[.
b) Montrer que 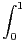 et lntd t = -
et lntd t = -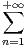
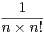 .
.
a) Trouver la solution générale de (E) sur R+* et R-*à l’aide du changement de fonction z = x2 y.
b) Pour une solution de (E) sur R, calculer la valeur en 0. Donner le développement en série
entière de x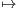
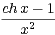 sur R*.
sur R*.
e) Montrer que la fonction précédente se prolonge en une solution de (E) sur R.
b) Soit (an )n N une suite réelle. On suppose que la série de terme général an est absolument
convergente. Trouver les solutions de yʹʹ + y =
N une suite réelle. On suppose que la série de terme général an est absolument
convergente. Trouver les solutions de yʹʹ + y = 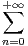 an cos(nx).
an cos(nx).
 R2
R2 x4 + y3 - 3y - 2.
x4 + y3 - 3y - 2.
 x4 + y4 - 2(x - y)2. Trouver les extrema locaux de f.
x4 + y4 - 2(x - y)2. Trouver les extrema locaux de f.
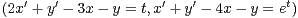 .
Écrire (S) sous la forme Xʹ = AX + B, où X est une matrice colonne. Résoudre le
système
.
Écrire (S) sous la forme Xʹ = AX + B, où X est une matrice colonne. Résoudre le
système
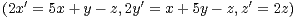 .
.
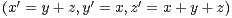 .
.
 N*, on note Fn
l’événement : ≪ le fumeur fume le jour n≫ et pn = P(Fn). Lorsque le fumeur fume un certain
jour, il ne fume pas le jour suivant avec une probabilité 1⁄4. S’il ne fume pas un certain jour, il fume
le lendemain avec la probabilité 1⁄2.
N*, on note Fn
l’événement : ≪ le fumeur fume le jour n≫ et pn = P(Fn). Lorsque le fumeur fume un certain
jour, il ne fume pas le jour suivant avec une probabilité 1⁄4. S’il ne fume pas un certain jour, il fume
le lendemain avec la probabilité 1⁄2.
a) Traduire ces hypothèses en termes de probabilité. Trouver une relation de récurrence vérifiée par (pn ). En déduire une expression de pn et la limite de (pn).
b) On suppose que p1 = 11⁄12. On fait de plus les deux hypothèses supplémentaires suivantes. Si le fumeur fume le premier jour, il fume les deux jours suivants avec une probabilité de 1⁄2. S’il fume le premier jour, il fume le troisième jour avec une probabilité de 1⁄4. Calculer la probabilité que le fumeur fume le premier et le troisième jour, la probabilité qu’il fume les trois premiers jours, la probabilité qu’il fume l’un des trois premiers jours.
 N,
N,
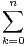 kP(X = k) =
kP(X = k) = 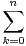 P(X > k) - (n + 1)P(X > n). En déduire une expression de E(X).
Comparer la nature des séries de termes généraux (kP(X = k))k et (P(X > k))k.
P(X > k) - (n + 1)P(X > n). En déduire une expression de E(X).
Comparer la nature des séries de termes généraux (kP(X = k))k et (P(X > k))k.
 R,
R,
P(X ≥ d) ≤ inf t>0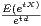 .
.
b) Soit p  ]0, 1[. Soit Xn une variable aléatoire suivant une loi binomiale
]0, 1[. Soit Xn une variable aléatoire suivant une loi binomiale 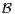 (n,p). Que donne
l’inégalité précédente pour Xn et d = αn ?
(n,p). Que donne
l’inégalité précédente pour Xn et d = αn ?
 ]0,1[. Pour n
]0,1[. Pour n  N*, on note Tn la variable aléatoire donnant le rang du
nième succès.
N*, on note Tn la variable aléatoire donnant le rang du
nième succès.
a) Expliciter la loi de T1.
b) Déterminer la loi de Tn.
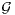 (p), U = max {X,Y }, V = min{X,Y }.
(p), U = max {X,Y }, V = min{X,Y }.
a) Déterminer les lois de U,V , (U,V ).
b) Déterminer la loi de U + V .
c) Calculer E(U + V ).
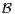 (n,p) et
(n,p) et
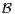 (nʹ, pʹ). À quelle condition X + Y suit-elle une loi binomiale ? À quelle condition supplémentaire
n - X + Y suit-elle aussi une loi binomiale ?
(nʹ, pʹ). À quelle condition X + Y suit-elle une loi binomiale ? À quelle condition supplémentaire
n - X + Y suit-elle aussi une loi binomiale ?
 ]0,1[ et (Xn) une suite de variables aléatoires mutuellement indépendantes
de même loi donnée par Xi(Ω) = {-1,1}, P(Xi = 1) = p et P(Xi = -1) = 1 - p. On pose
Zn =
]0,1[ et (Xn) une suite de variables aléatoires mutuellement indépendantes
de même loi donnée par Xi(Ω) = {-1,1}, P(Xi = 1) = p et P(Xi = -1) = 1 - p. On pose
Zn = 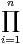 Xi. Calculer la loi de Zn.
Xi. Calculer la loi de Zn.
 ]0,1[. Soient p
]0,1[. Soient p  N* et s1,…,sp
N* et s1,…,sp  {0,1}. Soit
Bn =
{0,1}. Soit
Bn = 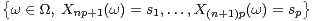 .
.
a) Montrer que les Bn sont mutuellement indépendants.
b) Déterminer l’événement contraire de ⋂
k N
N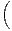 ⋃
i≥kBi
⋃
i≥kBi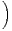 .
.
c) Montrer que, pour tout k  N, P
N, P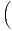 ⋂
i≥kBi
⋂
i≥kBi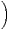 = 0.
= 0.
d) En déduire que P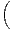 ⋂
k
⋂
k N
N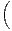 ⋃
i≥kBi
⋃
i≥kBi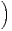
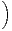 = 1 et interpréter le résultat.
= 1 et interpréter le résultat.
 ]0,1[. On définit
Z = X⁄Y .
]0,1[. On définit
Z = X⁄Y .
a) Justifier Z(Ω) ⊂ Q+*. Soit r  Q+* un rationnel d’écriture irréductible r = a⁄b. Montrer que
P(Z = r) =
Q+* un rationnel d’écriture irréductible r = a⁄b. Montrer que
P(Z = r) = 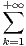 P(X = ka,Y = kb).
P(X = ka,Y = kb).
b) Justifier E(Z) = E(X)E(1⁄Y ). Calculer E(X), E(1⁄Y ) et en déduire E(Z).
c) Justifier l’inégalité lnx < x - 1 pour x > 0 et x≠1. En déduire E(Z) > 1. Que dire de ce résultat ?
[Épreuves orales des concours]

