[Table des matières]
Agrégation Interne de Mathématiques
Première preuve 2017
7037Racine carrée d’une matrice complexe
xistence et unicité pour une matrice carrée complexe A sans valeur propre réelle négative de 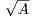 ,
racine carrée de A dont toute valeur propre est de partie réelle strictement positive. Preuve
d’appartenance de
,
racine carrée de A dont toute valeur propre est de partie réelle strictement positive. Preuve
d’appartenance de 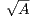 à l’algèbre de A. Mise en place d’une méthode itérative de calcul de
à l’algèbre de A. Mise en place d’une méthode itérative de calcul de 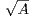 .
Projection orthogonale d’une matrice carrée réelle sur le groupe orthogonal, d’une matrice carrée
complexe sur le groupe unitaire.
.
Projection orthogonale d’une matrice carrée réelle sur le groupe orthogonal, d’une matrice carrée
complexe sur le groupe unitaire.
Préambule : notations et rappels
On désigne par N l’ensemble des entiers naturels. On désigne par R le corps des nombres réels, C le corps des nombres complexes et K l’un de ces deux corps lorsqu’on ne souhaite pas le préciser.
On désigne par R + l’ensemble des nombres réels positifs ou nuls, et par R- l’ensemble des nombres réels négatifs ou nuls.
Soit n un entier naturel non nul. On note  n(K) la K-algèbre des matrices (n,n) à coefficients
dans K et In la matrice identité dans
n(K) la K-algèbre des matrices (n,n) à coefficients
dans K et In la matrice identité dans  n(K). On note GLn(K) l’ensemble des matrices inversibles
dans
n(K). On note GLn(K) l’ensemble des matrices inversibles
dans  n (K ).
n (K ).
Sur  n (K ), on note Tr l’application trace.
n (K ), on note Tr l’application trace.
Soit M une matrice dans  n(K). On note Sp(M) le spectre de M, c’est-à-dire l’ensemble des
valeurs propres complexes de M.
n(K). On note Sp(M) le spectre de M, c’est-à-dire l’ensemble des
valeurs propres complexes de M.
Soit M dans  n (K) ; on note t M sa matrice transposée. Lorsque K = C, on note M* sa
matrice adjointe, i.e. M* = t M.
n (K) ; on note t M sa matrice transposée. Lorsque K = C, on note M* sa
matrice adjointe, i.e. M* = t M.
On rappelle qu’une matrice M symétrique dans  n(R) ou hermitienne dans
n(R) ou hermitienne dans  n(C) est dite
positive (respectivement définie positive) lorsque toutes ses valeurs propres sont positives ou nulles
(respectivement strictement positives).
n(C) est dite
positive (respectivement définie positive) lorsque toutes ses valeurs propres sont positives ou nulles
(respectivement strictement positives).
On note Un (K ) l’ensemble des matrices M dans  n(K) telles que M*M = In. Ainsi Un(R)
désigne le groupe orthogonal et Un(C) le groupe unitaire.
n(K) telles que M*M = In. Ainsi Un(R)
désigne le groupe orthogonal et Un(C) le groupe unitaire.
On rappelle que Un(R) contient les matrices P (dites de rotation plane) définies, pour (i0,j0) tel
que 1 ≤ i0 < j0 ≤ n et θ  R, de la façon suivante :
R, de la façon suivante :
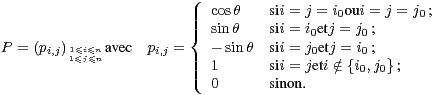
Dans tout le problème, on considère les sous-ensembles de C suivants :
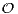 + est le demi-plan ouvert des nombres complexes de partie réelle > 0 ;
+ est le demi-plan ouvert des nombres complexes de partie réelle > 0 ; 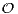 - le demi-plan ouvert des nombres complexes de partie réelle < 0 ;
- le demi-plan ouvert des nombres complexes de partie réelle < 0 ; 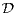 le disque unité ouvert de C, c’est-à-dire l’ensemble des nombres complexes de module
< 1.
le disque unité ouvert de C, c’est-à-dire l’ensemble des nombres complexes de module
< 1.
Pour tout nombre complexe z, on note Re(z) sa partie réelle.
1. Soit z un nombre complexe qui n’est pas un nombre réel négatif ou nul (z  C \ R-).
Démontrer qu’il existe un unique nombre complexe dans
C \ R-).
Démontrer qu’il existe un unique nombre complexe dans 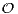 + noté
+ noté 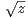 , tel que (
, tel que (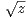 )2
= z.
)2
= z.
2. Soit g la fonction de la variable complexe z définie sur C \{-1} par :
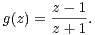
a) Démontrer que g(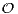 +) ⊂
+) ⊂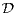 .
.
b) Démontrer que g réalise une bijection de 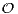 + sur
+ sur 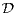 . Expliciter la bijection inverse.
. Expliciter la bijection inverse.
3. On définit sur  n(R) l’application N en posant, pour M dans
n(R) l’application N en posant, pour M dans  n(R),
n(R),
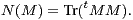
a) Soit M dans  n(R) telle que M = (mi,j). Justifier que tMM est une matrice symétrique
positive, qui est définie positive si M est inversible.
n(R) telle que M = (mi,j). Justifier que tMM est une matrice symétrique
positive, qui est définie positive si M est inversible.
b) Justifier que N est le carré d’une norme euclidienne sur  n(R). Expliciter le produit scalaire
euclidien < , > défini par :
n(R). Expliciter le produit scalaire
euclidien < , > défini par :
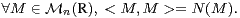
4. Expliciter un produit hermitien sur  n(C) tel que la norme associée, notée Nʹ,
vérifie :
n(C) tel que la norme associée, notée Nʹ,
vérifie :
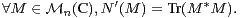
5. Soit L une matrice dans  n(K) telle que L2 = In.
n(K) telle que L2 = In.
a) Démontrer qu’il existe des sous-espaces vectoriels F et G de Kn tels que :
- Kn= F ⊕ G ;
- ∀x
 F, Lx = x ;
F, Lx = x ;
- ∀x
 G, Lx = -x.
G, Lx = -x.
b) Démontrer que Tr(L) = dimF - dimG.
6. Soit 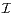 n l’ensemble des matrices L dans
n l’ensemble des matrices L dans  n(K) telle que L2 = In. On définit sur
n(K) telle que L2 = In. On définit sur 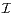 n la relation
~ par :
n la relation
~ par :
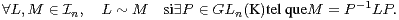
a) Démontrer que ~ est une relation d’équivalence sur 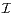 n.
n.
b) Soient L et M deux matrices dans 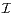 n. Démontrer que :
n. Démontrer que :
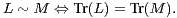
c) Justifier que la relation ~ n’a qu’un nombre fini de classes d’équivalence. Déterminer ce nombre.
Soit n un entier naturel non nul. Soit A une matrice dans  n(C) telle que le spectre de A,
n(C) telle que le spectre de A, 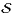 p(A),
est contenu dans
p(A),
est contenu dans 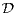 . On se propose de démontrer qu’alors la suite (Al)l
. On se propose de démontrer qu’alors la suite (Al)l N converge dans
N converge dans  n(C)
vers la matrice nulle.
n(C)
vers la matrice nulle.
7. On suppose que A admet une unique valeur propre α. On pose B = A - αIn.
a) Justifier que Bn = 0.
b) Soit l un entier naturel non nul. Exprimer Al en fonction de I,B,...,Bn-1.
c) En déduire que la suite (Al)l N converge dans
N converge dans  n(C) vers la matrice nulle.
n(C) vers la matrice nulle.
8. Dans le cas général, démontrer que la suite (Al)l N converge dans
N converge dans  n(C) vers la matrice
nulle.
n(C) vers la matrice
nulle.
Soit f la fonction définie sur C* par f(z) = 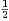
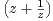 .
.
Pour α dans C * , on considère la suite récurrente uα = (ul)l N définie par :
N définie par :
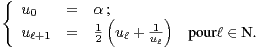
Lorsque la suite uα est bien définie (c’est-à-dire si ul est défini pour tout entier naturel l) et que de plus elle converge dans C, sa limite est notée sα.
9. Donner une valeur non nulle de α telle que la suite uα n’est pas bien définie.
10. Soit α un nombre réel non nul. Démontrer que la suite uα = (ul)l N est bien définie. tudier la
monotonie de la suite uα et démontrer qu’elle converge. Expliciter la valeur de sα en fonction de
α.
N est bien définie. tudier la
monotonie de la suite uα et démontrer qu’elle converge. Expliciter la valeur de sα en fonction de
α.
11. a) Justifier que les demi-plans 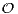 + et
+ et 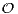 - sont stables par f. En déduire que si α n’est pas un
imaginaire pur, la suite uα = (ul)l
- sont stables par f. En déduire que si α n’est pas un
imaginaire pur, la suite uα = (ul)l N est bien définie.
N est bien définie.
b) Soit β un nombre complexe de module différent de 1. Pour tout entier naturel l, on pose :
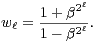
 N converge et déterminer sa
limite.
N converge et déterminer sa
limite.
c) On suppose que α n’est pas un imaginaire pur. Justifier que la suite uα = (ul)l N converge.
Expliciter la valeur de sα en fonction de α.
N converge.
Expliciter la valeur de sα en fonction de α.
Soit n un entier naturel tel que n ≥ 2.
Soit A une matrice inversible dans  n(C). On note
n(C). On note 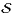 p(A) le spectre de A, c’est-à-dire l’ensemble
des valeurs propres de A. On s’intéresse dans le problème à l’éventuelle limite de la suite
UA = (Ul )l
p(A) le spectre de A, c’est-à-dire l’ensemble
des valeurs propres de A. On s’intéresse dans le problème à l’éventuelle limite de la suite
UA = (Ul )l N définie par :
N définie par :
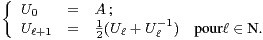
12. On suppose, dans cette question seulement, la matrice A diagonalisable. On suppose de plus
que son spectre 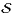 p(A) satisfait la propriété :
p(A) satisfait la propriété :
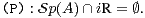
a) Démontrer que la suite récurrente UA = (Ul)l N est bien définie.
N est bien définie.
b) Démontrer que la suite récurrente UA converge. Justifier que LA est une matrice diagonalisable
telle que 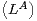 2 = In.
2 = In.
c) Démontrer que la suite 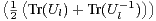 l
l N converge vers un nombre entier qu’on
explicitera en fonction des valeurs propres de A.
N converge vers un nombre entier qu’on
explicitera en fonction des valeurs propres de A.
13. On suppose ici que la matrice A vérifie la propriété :
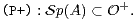
a) Justifier que la matrice 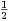
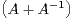 vérifie la propriété (P+). En déduire que la
suite UA = (Ul )l
vérifie la propriété (P+). En déduire que la
suite UA = (Ul )l N est bien définie et que chacune des matrices Ul vérifie la propriété
(P+).
N est bien définie et que chacune des matrices Ul vérifie la propriété
(P+).
b) Soit α une valeur propre de la matrice (A-In)(A + In)-1. Démontrer qu’il existe β une valeur propre de A telle que g(β) = α (où g est la fonction définie dans les préliminaires).
c) Démontrer que, pour tout entier naturel l,
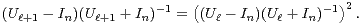
d) Justifier que la suite 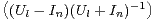 l
l N converge dans
N converge dans  n(C) vers la matrice
nulle.
n(C) vers la matrice
nulle.
e) En déduire la convergence de la suite UA = (Ul)l N. Expliciter LA.
N. Expliciter LA.
14. Lorsque la matrice A vérifie la propriété :
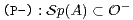
 N et expliciter LA.
N et expliciter LA.
15. On suppose ici que la matrice A vérifie la propriété :
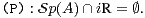
a) On suppose de plus dans cette question que la matrice A ne vérifie ni la propriété (P+) ni la propriété (P-) . Démontrer qu’il existe une matrice inversible P et deux matrices carrées C et D telles que :
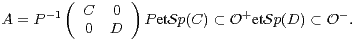
b) En déduire la convergence de la suite UA = (Ul)l N. Expliciter les valeurs propres de
LA .
N. Expliciter les valeurs propres de
LA .
Soit A une matrice dans  n(C). On suppose dans cette partie que la matrice A vérifie la
propriété :
n(C). On suppose dans cette partie que la matrice A vérifie la
propriété :
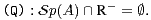
On définit la matrice B dans  2n(C) en posant :
2n(C) en posant :
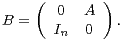
16. Déterminer les valeurs propres de la matrice B en fonction des valeurs propres de A. On précisera leurs multiplicités en fonction des multiplicités des valeurs propres de A.
17. Justifier que la matrice B vérifie la propriété (P) (définie dans la partie IV) et en déduire que la suite UB converge.
18. Démontrer que les termes de la suite UB vérifient :
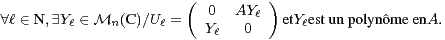
19. En déduire qu’il existe une matrice L dans  n(C) telle que :
n(C) telle que :
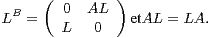
20. Démontrer qu’il existe une unique matrice notée 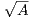 qui vérifie la propriété (P+) et telle
que :
qui vérifie la propriété (P+) et telle
que :
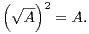
21. Lorsque A est une matrice réelle symétrique (respectivement une matrice complexe
hermitienne) définie positive, justifier l’existence de 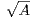 et démontrer que
et démontrer que 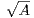 est une
matrice réelle symétrique (respectivement une matrice complexe hermitienne) définie
positive.
est une
matrice réelle symétrique (respectivement une matrice complexe hermitienne) définie
positive.
Dans cette partie, K = R.
22. Justifier que Un(R) est un compact de  n(R).
n(R).
23. Soit M dans  n(R). Démontrer qu’il existe une matrice P0 dans Un(R) telle
que :
n(R). Démontrer qu’il existe une matrice P0 dans Un(R) telle
que :
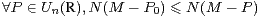
24. Soit M dans  n(R). Soit P0 une matrice dans Un(R). Démontrer l’équivalence des
assertions :
n(R). Soit P0 une matrice dans Un(R). Démontrer l’équivalence des
assertions :
- ∀P
 Un (R),N(M - P0) ≤ N(M - P);
Un (R),N(M - P0) ≤ N(M - P);
- ∀P
 Un (R),Tr(tPM) ≤ Tr(tP0M);
Un (R),Tr(tPM) ≤ Tr(tP0M);
- ∀P
 Un (R),N(M + P) ≤ N(M + P0).
Un (R),N(M + P) ≤ N(M + P0).
25. Soit M dans  n(R) symétrique définie positive. Justifier que la seule matrice P0 dans Un(R)
réalisant : ∀P
n(R) symétrique définie positive. Justifier que la seule matrice P0 dans Un(R)
réalisant : ∀P  Un(R),N(M -P0) ≤ N(M -P), est P0 = In. On pourra exprimer, pour P
dans Un (R ), Tr (t PM) sur une base bien choisie.
Un(R),N(M -P0) ≤ N(M -P), est P0 = In. On pourra exprimer, pour P
dans Un (R ), Tr (t PM) sur une base bien choisie.
26. Réciproquement, soit M dans  n(R) telle que : ∀P
n(R) telle que : ∀P  Un(R),N(M -In) ≤ N(M -P).
Un(R),N(M -In) ≤ N(M -P).
a) On suppose M non symétrique. Justifier qu’il existe une matrice de rotation plane (dont la définition est rappelée dans le préambule) P telle que Tr(PM) > Tr(M). En déduire que M est symétrique.
b) Soit v un vecteur de Rn de norme 1. On note Pv la matrice In - 2vtv.
- Démontrer que Pv
 Un(R).
Un(R).
- Démontrer que Tr(PvM) = Tr(M) - 2 < v,Mv > où < , > désigne ici le produit scalaire canonique de Rn.
c) Démontrer que M est symétrique positive.
d) Soit M dans  n(R) telle que la seule matrice P0 dans Un(R) réalisant : ∀P
n(R) telle que la seule matrice P0 dans Un(R) réalisant : ∀P  Un(R),
N(M - In ) ≤ N(M - P), est P0 = In. Démontrer que M est symétrique définie
positive.
Un(R),
N(M - In ) ≤ N(M - P), est P0 = In. Démontrer que M est symétrique définie
positive.
27. Soit M inversible dans  n(R).
n(R).
a) Justifier qu’il existe une matrice Q0 dans Un(R) telle que : M = Q0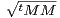 (cf. question
21).
(cf. question
21).
b) Démontrer qu’une telle matrice Q0 est l’unique matrice P0 dans Un(R) qui vérifie :
∀P  Un (R ), N(M - P0) ≤ N(M - P).
Un (R ), N(M - P0) ≤ N(M - P).
28. Pourrait-on avoir l’unicité d’un tel P0 lorsque la matrice M n’est pas inversible ?
29. Soient A0 et V 0 deux matrices dans  n(C) telles que A0 est une matrice antihermitienne et
V 0 une matrice unitaire. Soit γ l’application définie par :
n(C) telles que A0 est une matrice antihermitienne et
V 0 une matrice unitaire. Soit γ l’application définie par :
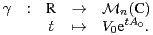
 ∞ de R à valeurs dans Un(C). Expliciter
γ(0), γʹ(0) et γʹʹ (0).
∞ de R à valeurs dans Un(C). Expliciter
γ(0), γʹ(0) et γʹʹ (0).
30. Soit M inversible dans  n(C) . Soit η l’application définie par :
n(C) . Soit η l’application définie par :
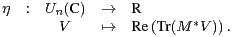
a) Soit A0 une matrice antihermitienne dans  n(C). Justifier que :
n(C). Justifier que :
- Re
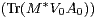 = 0 ;
= 0 ;
- Re
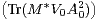 ≤ 0.
≤ 0.
b) En déduire que M*V 0 est une matrice hermitienne définie positive.
31. Soit M inversible dans  n(C) . Justifier qu’il existe une unique matrice V 0 dans Un(C) telle
que M = V 0
n(C) . Justifier qu’il existe une unique matrice V 0 dans Un(C) telle
que M = V 0 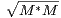 .
.
FIN DU SUJET
[Table des matières]

