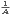[Table des matières]
Théorème de Korenbljum et problème des moments discrets
par Rafik Imekraz et Hervé Queffélec
Maître de Conférences, rafik.imekraz@math.u-bordeaux.fr
Université de Bordeaux, Institut de Mathématiques de Bordeaux, UMR 5251
Professeur émérite, herve.queffelec@univ-lille1.fr
Université de Lille 1, Laboratoire Paul Painlevé, UMR 8524
Résumé. On montre des liens entre un théorème de classes quasi-analytiques et un problème de moments de variables aléatoires discrètes.
Abstract. Korenbljum theorem and a discret moment problem
We study the relationship between a theorem dealing with quasi-analytic classes and a problem about moments of discrete random variables.
Mots-clés : Denjoy-Carleman, Korenbljum, classes quasi-analytiques, moments, suite log-convexe.
Dans cette note intervient plusieurs fois la notion de suite log-convexe dont on rappelle la définition :
Définition 1.Une suite strictement positive (Mk)k N est log-convexe si l’on dispose de
l’inégalité M
N est log-convexe si l’on dispose de
l’inégalité M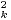 ≤ Mk-1Mk+1 pour tout k
≤ Mk-1Mk+1 pour tout k  N⋆.
N⋆.
Par exemple, la suite de terme général Mk = k!α est log-convexe pour tout réel α > 0. Cette notion intervient classiquement dans l’étude des classes quasi-analytiques pour lesquelles on renvoie le lecteur à [1,3,4]. En fait, la principale motivation de cette note est de donner des versions quantitatives d’un problème de moments qui apparaît dans la rubrique QR (voir la réponse R897 de la présente revue). Afin d’unifier plusieurs énoncés, on se permet d’introduire la notion suivante :
Définition 2.Soit (Mk) une suite log-convexe. On dira qu’une suite complexe (uk)k N est à
croissance de type (Mk) si
N est à
croissance de type (Mk) si
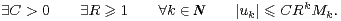 |
Par exemple, une suite à croissance de type (1) est tout simplement à croissance au plus exponentielle.
Pour toute fonction f : R → C, on utilisera la notation usuelle ∥f∥∞ = supx R
R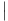 f(x)
f(x)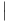 . De même,
Edésignera l’opérateur usuel d’espérance dans la théorie des probabilités. Voici le théorème que
nous allons démontrer.
. De même,
Edésignera l’opérateur usuel d’espérance dans la théorie des probabilités. Voici le théorème que
nous allons démontrer.
Théorème 1.Soit (Mk)k N une suite strictement positive et log-convexe. Les propriétés
suivantes sont équivalentes :
N une suite strictement positive et log-convexe. Les propriétés
suivantes sont équivalentes :
- 1)
- la série
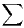
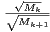 est convergente ;
est convergente ;
- 2)
- la série
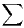
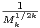 est convergente ;
est convergente ;
- 3)
- il existe deux variables aléatoires X et Y , de lois distinctes, à valeurs dans N vérifiant
E[Xk ] = E[Y k] pour tout k
 N et telles que la suite (E[Xk])k
N et telles que la suite (E[Xk])k N est à croissance
de type (Mk) ;
N est à croissance
de type (Mk) ;
- 4)
- il existe une suite complexe non nulle (an)n
 N vérifiant
N vérifiant 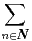 annk = 0 pour tout k
annk = 0 pour tout k  N
et telle que la suite
N
et telle que la suite 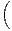
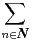 nk|an|
nk|an| k est à croissance de type (Mk) ;
k est à croissance de type (Mk) ;
- 5)
- il existe une fonction F

 ∞(R,C) non nulle, 2π-périodique dont le développement en série
de Fourier est de la forme
∞(R,C) non nulle, 2π-périodique dont le développement en série
de Fourier est de la forme
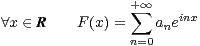
telle que toutes les les dérivées de F s’annulent en 0 (on dit que F est plate en 0) et que la suite
 ∥F(k)∥∞
∥F(k)∥∞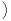 k
k N est à croissance de type (Mk).
N est à croissance de type (Mk).
Par exemple, avec la suite Mk = k!α avec α > 2, le point 3) du théorème précédent donne un éclairage de la réponse R897. Ainsi, on peut avoir E[Xk]1⁄k ≲ kα mais le cas α = 2 est interdit. Nous donnerons aussi une preuve auto-contenue de l’assertion 5) dans le cas où Mk = k!α avec α > 2.
Le sens des preuves sera le suivant : 5) ⇒ 4) ⇒ 3) ⇒ 5) ⇔ 1) ⇔ 2)
L’équivalence 1) ⇔ 5) est connue sous le nom de théorème de Korenbljum [2]. Il s’agit d’une variante ≪ analytique-trigonométrique ≫ du théorème de Denjoy-Carleman que nous utiliserons et admettrons [4, Théorèmes 19.10 et 19.11] :
Théorème 2.Soit (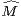 k)k
k)k N une suite strictement positive et log-convexe ; les propriétés suivantes
sont alors équivalentes :
N une suite strictement positive et log-convexe ; les propriétés suivantes
sont alors équivalentes :
- la série
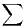
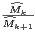 est convergente ;
est convergente ;
- il existe une fonction f

 ∞(R,C) non nulle, dont toutes les dérivées s’annulent en 0
et telle que la suite
∞(R,C) non nulle, dont toutes les dérivées s’annulent en 0
et telle que la suite 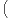 ∥f(k)∥∞
∥f(k)∥∞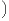 k
k N est à croissance de type (
N est à croissance de type (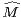 k).
k).
On pourra consulter des variantes L2 et 2π-périodiques dans [1, Chapter V]. L’approche présentée ici est différente de celle de [2] en ce sens que nous montrons que le théorème de Korenbljum peut directement se déduire du théorème de Denjoy-Carleman. Même si nous ne l’écrirons pas, notre approche permet sans doute d’obtenir le sens réciproque, à savoir que le théorème de Korenbljum devrait impliquer le théorème de Denjoy-Carleman.
Signalons pour finir cette introduction qu’il existe une forme légèrement plus générale du théorème
de Denjoy-Carleman qui s’émancipe de la notion de log-convexité [3, p. 101-102]. En l’occurrence,
si l’on se donne une suite strictement positive et croissante (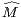 n)n≥0, alors on peut remplacer
l’assertion 1) du théorème 2 par
n)n≥0, alors on peut remplacer
l’assertion 1) du théorème 2 par
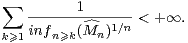 |
Cela simplifierait certaines preuves de la présente note.
Dans ce qui suit, la lettre C désignera une constante strictement positive qui peut changer d’une ligne à l’autre.
1.Algèbre lisse du disque et fonctions presque-périodiques
Pour passer d’un théorème de classe quasi-analytique à l’autre, nous allons introduire deux espaces
fonctionnels notés ci-après 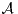 ∞(R) et
∞(R) et 
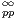 (R).
(R).
Définissons tout d’abord l’algèbre lisse du disque 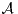 ∞(R), c’est-à-dire l’algèbre des
fonctions de classe
∞(R), c’est-à-dire l’algèbre des
fonctions de classe  ∞, 2π-périodiques sur R, qui admettent un développement en série de
Fourier
∞, 2π-périodiques sur R, qui admettent un développement en série de
Fourier
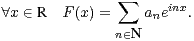 | (1) |
Par application du théorème de Parseval-Bessel aux dérivées de F , on constate que (an) est nécessairement à décroissance rapide en ce sens que
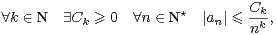 |
et réciproquement cela suffit pour obtenir un élément de  ∞(R) à partir de la formule (1).
Rappelons que sans la régularité
∞(R) à partir de la formule (1).
Rappelons que sans la régularité  ∞, la terminologie ≪ algèbre du disque ≫ vient du fait qu’une
fonction F comme précédemment est usuellement vue comme la restriction au cercle
trigonométrique de la fonction z
∞, la terminologie ≪ algèbre du disque ≫ vient du fait qu’une
fonction F comme précédemment est usuellement vue comme la restriction au cercle
trigonométrique de la fonction z
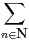 anzn qui est par ailleurs holomorphe sur le disque ouvert
unité et continue sur la fermeture de ce disque.
anzn qui est par ailleurs holomorphe sur le disque ouvert
unité et continue sur la fermeture de ce disque.
Passons maintenant à la définition de 
 (R). Il s’agira ici du C-espace vectoriel des
fonctions f : R → C pour lesquelles il existe une suite (an)n
(R). Il s’agira ici du C-espace vectoriel des
fonctions f : R → C pour lesquelles il existe une suite (an)n N à décroissance rapide telle
que
N à décroissance rapide telle
que
 | (2) |
On notera que, d’après la théorie des séries de Fourier, l’espace 
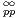 (R) contient les fonctions à la
fois paires, 2π-périodiques et de classe
(R) contient les fonctions à la
fois paires, 2π-périodiques et de classe  ∞ sur R (cette remarque sera clarifiée plus loin avec la
théorie des fonctions presque-périodiques).
∞ sur R (cette remarque sera clarifiée plus loin avec la
théorie des fonctions presque-périodiques).
De façon générale, une fonction f appartenant à 
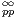 (R) vérifie les propriétés suivantes :
(R) vérifie les propriétés suivantes :
- elle est de classe
 ∞,
∞,
- elle est paire,
- elle est bornée ainsi que toute ses dérivées.
On a en outre la propriété suivante (la seule propriété de 
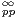 (R) dont on aura besoin) :
(R) dont on aura besoin) :
Démonstration La seule hypothèse que nous allons utiliser est la convergence absolue
de la série 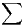 an qui entraîne que, pour tout réel T > 0, par convergence normale sur
[0, T] :
an qui entraîne que, pour tout réel T > 0, par convergence normale sur
[0, T] :
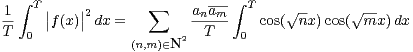 | (4) |
et
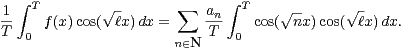 | (5) |
En invoquant la formule
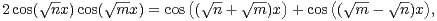 |
on obtient par calcul direct
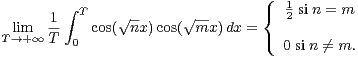 | (6) |
Ce qui suggère que l’on doit avoir
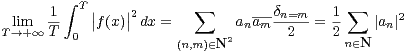 |
et
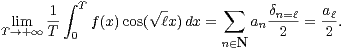 |
Cela est une conséquence immédiate du théorème de la convergence normale et d’une interversion
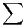 lim = lim
lim = lim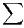 en considérant les séries de fonctions (4) et (5) sur [0,+∞[.
en considérant les séries de fonctions (4) et (5) sur [0,+∞[.
cqfd
Bien que cela ne soit pas nécessaire au niveau des démonstrations, il est intéressant de noter que la
théorie des fonctions presque-périodiques (voir [5]) permet de donner un éclairage de toutes les
propriétés précédentes. En effet, les fonctions f 

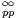 (R) sont presque-périodiques à spectre inclus
dans Λ := {±
(R) sont presque-périodiques à spectre inclus
dans Λ := {±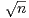 ,n
,n  N}. La réciproque est vraie : si f vérifie les propriétés i), ii) et iii) et
est presque-périodique à spectre inclus dans Λ alors f appartient à
N}. La réciproque est vraie : si f vérifie les propriétés i), ii) et iii) et
est presque-périodique à spectre inclus dans Λ alors f appartient à 
 (R). En effet,
si f est presque-périodique alors on peut lui associer un développement en ≪ série de
Fourier ≫
(R). En effet,
si f est presque-périodique alors on peut lui associer un développement en ≪ série de
Fourier ≫ 
 αnei
αnei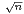 x
+ βne-i
x
+ βne-i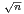 x
x
 . Par parité, ce dernier se ramène à un développement de la
forme
. Par parité, ce dernier se ramène à un développement de la
forme 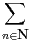 an cos(
an cos(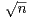 x). Ensuite, fʹétant uniformément continue grâce à iii), la théorie des
fonctions presque-périodiques assure alors que fʹ est aussi presque-périodique et que
son développement en série de Fourier est obtenu en dérivant terme à terme celui de f.
Une récurrence évidente amène aux développements convergents suivants pour tout
k
x). Ensuite, fʹétant uniformément continue grâce à iii), la théorie des
fonctions presque-périodiques assure alors que fʹ est aussi presque-périodique et que
son développement en série de Fourier est obtenu en dérivant terme à terme celui de f.
Une récurrence évidente amène aux développements convergents suivants pour tout
k  N :
N :
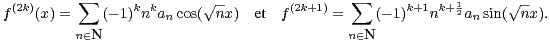 |
On dispose en outre d’un théorème de Parseval-Bessel comme dans la proposition 1. Cela implique que la suite (an ) est à décroissance rapide. Par unicité du développement en série de Fourier, on obtient alors l’égalité
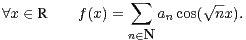 |
Fermons à présent la parenthèse sur les fonctions presque-périodiques et venons-en au lien entre les
deux espaces 
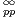 (R) et
(R) et 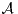 ∞(R). D’après la formule (3), la décomposition d’une fonction
f
∞(R). D’après la formule (3), la décomposition d’une fonction
f 

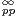 (R ) selon la famille de fonctions x
(R ) selon la famille de fonctions x cos(
cos(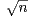 x) est unique. On peut donc manifestement
passer de
x) est unique. On peut donc manifestement
passer de 
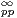 (R ) à
(R ) à 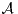 ∞(R) par le biais de l’isomorphisme d’espaces vectoriels défini
par
∞(R) par le biais de l’isomorphisme d’espaces vectoriels défini
par
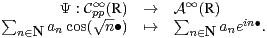 | (7) |
Nous pouvons énoncer le résultat suivant qui va faire le lien entre le théorème de Denjoy-Carleman et le théorème de Korenbljum :
Proposition 2.Soit f 

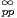 (R) et notons F := Ψ(f)
(R) et notons F := Ψ(f) 
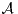 ∞(R). Alors les assertions suivantes sont
vraies :
∞(R). Alors les assertions suivantes sont
vraies :
- la fonction f est plate en 0 si seulement si F est plate en 0 ;
- pour tout k
 N on a
N on a 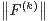 ∞ ≤ C
∞ ≤ C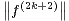 ∞ et
∞ et 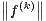 ∞ ≤ C
∞ ≤ C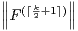 ∞,
où l’on désigne par ⌈k⁄2 + 1⌉ le plus petit entier supérieur ou égal à k⁄2 + 1.
∞,
où l’on désigne par ⌈k⁄2 + 1⌉ le plus petit entier supérieur ou égal à k⁄2 + 1.
Démonstration i) C’est immédiat (on notera que les dérivées impaires de f s’annulent trivialement en 0).
ii) On peut supposer k ≥ 1. Avec les notations précédentes et la proposition 1, on écrit
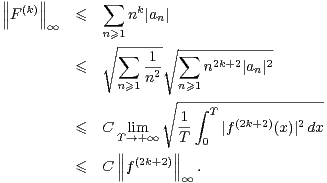
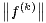 ∞. On peut dériver terme à terme (2) car (an)n
∞. On peut dériver terme à terme (2) car (an)n N est à
décroissance rapide. Le théorème de Parseval-Bessel pour la fonction F , définie en (1), nous mène
alors à
N est à
décroissance rapide. Le théorème de Parseval-Bessel pour la fonction F , définie en (1), nous mène
alors à 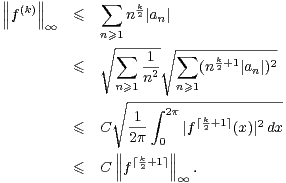
D’un point de vue technique nous avons besoin du lemme suivant.
Lemme 1.Soit (Mk) une suite strictement positive et log-convexe. Alors, la suite (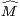 k)k
k)k N
définie par
N
définie par 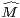 0 =
0 = 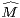 1 = M0 et :
1 = M0 et :
∀k ≥ 0, 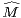 2k+2 = Mk, ∀k ≥ 1,
2k+2 = Mk, ∀k ≥ 1,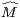 2k+1 =
2k+1 = 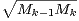
est strictement positive et log-convexe.
De plus, la série 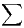
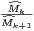 converge si et seulement si la série
converge si et seulement si la série 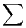
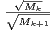 converge.
converge.
Démonstration Pour tout entier pair 2k + 2 ≥ 2, on pose 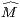 2k+2 = Mk. En ce qui concerne les
entiers impairs 2k + 1 ≥ 3, le meilleur choix pour garantir la log-convexité est de poser
2k+2 = Mk. En ce qui concerne les
entiers impairs 2k + 1 ≥ 3, le meilleur choix pour garantir la log-convexité est de poser
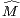 2k+1:=
2k+1:= 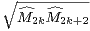 =
= 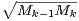 . Il reste néanmoins à vérifier la log-convexité dans le cas
pair :
. Il reste néanmoins à vérifier la log-convexité dans le cas
pair :
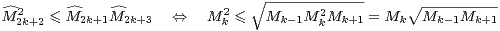 |
où le membre droit de l’équivalence est vrai par log-convexité de (Mk). Si l’on affecte à présent à
 0et
0et  1 la valeur M0, alors la log-convexité de (
1 la valeur M0, alors la log-convexité de (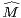 k)k
k)k N est bien vérifiée puisque l’on
a
N est bien vérifiée puisque l’on
a
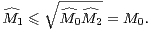 |
Il nous reste à étudier la convergence de la série 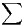
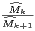 . Cela est immédiat en considérant les
deux sous-séries d’indices pairs et impairs :
. Cela est immédiat en considérant les
deux sous-séries d’indices pairs et impairs :
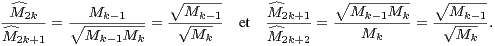 |
Cela achève la preuve du lemme. cqfd
2.Implication 1) ⇒ 5) du théorème 1
On part d’une suite log-convexe (Mk) vérifiant 1). Considérons la suite log-convexe (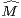 k) fournie
par le lemme 1. On fait alors appel au théorème de Denjoy-Carleman pour assurer l’existence d’une
fonction non nulle g
k) fournie
par le lemme 1. On fait alors appel au théorème de Denjoy-Carleman pour assurer l’existence d’une
fonction non nulle g 
 ∞(R, C) plate en 0 vérifiant
∞(R, C) plate en 0 vérifiant
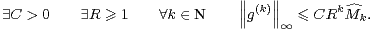 |
On souhaiterait alors appliquer l’isomorphisme Ψ défini en (7) à g afin d’obtenir une fonction qui
soit 2π-périodique et à fréquences incluses dans N. L’ennui est que g n’appartient pas à
l’espace vectoriel 
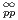 (R). Mais peu s’en faut ! En effet, on peut considérer la fonction
f : x
(R). Mais peu s’en faut ! En effet, on peut considérer la fonction
f : x  [0, π]
[0, π]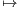 g(x)g(π - x) afin d’obtenir une fonction plate en 0 et π. Par suite, il suffit de
prolonger f en une fonction paire sur R et 2π-périodique. Il est clair que l’on obtient ainsi une
fonction de classe
g(x)g(π - x) afin d’obtenir une fonction plate en 0 et π. Par suite, il suffit de
prolonger f en une fonction paire sur R et 2π-périodique. Il est clair que l’on obtient ainsi une
fonction de classe  ∞ qui appartient à
∞ qui appartient à 
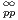 (R), et on peut facilement trouver des estimations des
normes
(R), et on peut facilement trouver des estimations des
normes 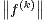 ∞ similaires à celles des
∞ similaires à celles des 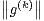 ∞, à l’aide de la formule de Leibniz et de
la log-convexité de la suite (
∞, à l’aide de la formule de Leibniz et de
la log-convexité de la suite (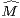 k) (voir l’argument de la preuve du théorème 19.7 de
[4]).
k) (voir l’argument de la preuve du théorème 19.7 de
[4]).
Par suite, la proposition 2 et le lemme 1 fournissent une fonction non nulle F = Ψ(f) 
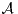 ∞(R)
plate en 0 qui vérifie
∞(R)
plate en 0 qui vérifie
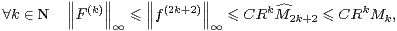 |
c’est-à-dire les estimations attendues dans l’assertion 5 du théorème 1.
Commentaire. Dans le cas Mk = k!α avec α > 2, on peut simplifier la démarche précédente en se
passant du lemme 1 et surtout du théorème de Denjoy-Carleman. Considérons en effet le réel A > 0
vérifiant α = 2 + 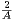 (cette condition intervient plus loin dans l’inégalité finale (8)) et la fonction
g
(cette condition intervient plus loin dans l’inégalité finale (8)) et la fonction
g 
 ∞ (R , R ) définie par g(x) = exp(-1⁄xA)1x>0. Par holomorphie, la formule de Cauchy
fournit les estimations suivantes :
∞ (R , R ) définie par g(x) = exp(-1⁄xA)1x>0. Par holomorphie, la formule de Cauchy
fournit les estimations suivantes :
Démonstration Il suffit d’estimer  g(k)(x)
g(k)(x) pour tout x > 0. Prolongeons g sur C\R- par la
formule g(z) := exp(-z-A) (où zA est la détermination principale de la fonction puissance
complexe). La formule de Cauchy assure que pour tout r
pour tout x > 0. Prolongeons g sur C\R- par la
formule g(z) := exp(-z-A) (où zA est la détermination principale de la fonction puissance
complexe). La formule de Cauchy assure que pour tout r  ]0,1[ on a
]0,1[ on a
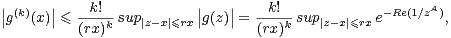 |
où l’on remarquera que le disque fermé {z  C,|z - x|≤ rx} est inclus dans le domaine de
définition de g. Par homogénéité, on a
C,|z - x|≤ rx} est inclus dans le domaine de
définition de g. Par homogénéité, on a
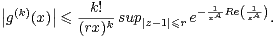 |
Par continuité de z zA en 1, il existe r > 0 suffisamment petit et c > 0 tels que
zA en 1, il existe r > 0 suffisamment petit et c > 0 tels que
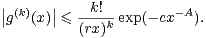 |
En développant en série entière l’exponentielle, on a 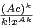 ≤ eAcx-A
et donc
≤ eAcx-A
et donc
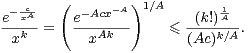 |
Il existe donc C > 0 et R ≥ 1 tels que l’on a  g(k)(x)
g(k)(x)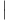 ≤ CRk(k!)1+
≤ CRk(k!)1+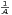 . cqfd
. cqfd
En partant de g : R → C par le même procédé que plus haut, on peut construire une fonction non
nulle f 
 ∞ (R , R), 2π-périodique, plate en 0, et dont les dérivées f(k) vérifient les mêmes
estimations que g(k). Par suite, on pose F = Ψ(f) qui est une fonction non nulle, plate en 0 et
vérifie
∞ (R , R), 2π-périodique, plate en 0, et dont les dérivées f(k) vérifient les mêmes
estimations que g(k). Par suite, on pose F = Ψ(f) qui est une fonction non nulle, plate en 0 et
vérifie
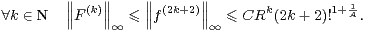 |
Or on peut invoquer l’inégalité triviale (2k)! ≤ k!24k (obtenue en examinant le développement du binôme de Newton sur (1 + 1)2k). Cela nous amène aux estimations
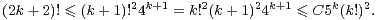 |
Quitte à changer C et R, on obtient donc
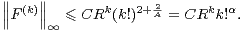 | (8) |
3.Implication 5) ⇒ 1) du théorème 1
Partons d’une suite log-convexe (Mk) et considérons une fonction non nulle F 
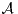 ∞(R), plate en
0 et vérifiant les estimations
∞(R), plate en
0 et vérifiant les estimations
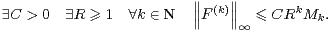 |
Notons f := Ψ-1 (F), qui est une fonction non nulle mais plate en 0. La proposition 2 nous donne alors
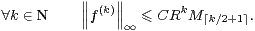 | (9) |
Nous proposons deux argumentations pour finir.
Première méthode. On note (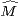 k) la suite log-convexe fournie par le lemme 1. Pour tout entier l, on
a alors
k) la suite log-convexe fournie par le lemme 1. Pour tout entier l, on
a alors
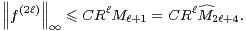 |
Pour estimer f(2l-1), on fait appel à une version faible de l’inégalité de Kolmogorov-Landau :
Démonstration On peut supposer que l’on a 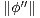 ∞ > 0. Pour tous x
∞ > 0. Pour tous x  R et h > 0, l’inégalité de
Taylor-Lagrange nous donne
R et h > 0, l’inégalité de
Taylor-Lagrange nous donne
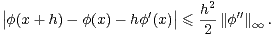
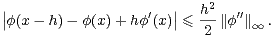
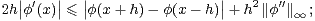
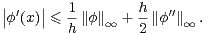 |
On conclut avec h = 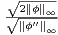 . cqfd
. cqfd
Pour ce qui nous concerne, nous obtenons
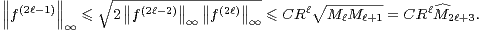 |
Autrement dit, la suite (∥f(k)∥∞) est à croissance de type (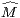 k+4). D’après le théorème de
Denjoy-Carleman, la série
k+4). D’après le théorème de
Denjoy-Carleman, la série 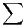
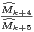 est convergente. Il en de même de la série
est convergente. Il en de même de la série 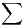
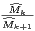 par
translation d’indices et de la série
par
translation d’indices et de la série 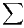
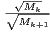 d’après le lemme 1.
d’après le lemme 1.
Seconde méthode. Nous allons utiliser la propriété suivante, que l’on attend de la log-convexité :
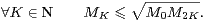 | (10) |
Cela se voit immédiatement en remarquant que la log-convexité signifie la décroissance de la suite
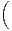
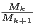
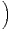 k≥0 et en écrivant
k≥0 et en écrivant
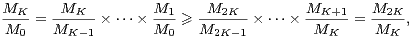 |
c’est-à-dire (10) . Quitte à changer C dans (9), on obtient
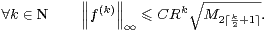 |
D’après le comportement asymptotique classiquement attendu pour une fonction convexe (voir le lemme 2 ci-après), on peut distinguer deux sous-cas :
∙ la suite (Mk ) est majorée, et dans ce cas f vérifie des estimations analytiques (associées à la suite log-convexe (1)). Sans même invoquer le théorème de Denjoy-Carleman, la théorie des fonctions holomorphes assure que f est forcément nulle. Ce qui est contradictoire.
∙ la suite (Mk ) est croissante à partir d’un certain rang. Dans ce cas, on invoque alors l’inégalité évidente 2⌈k⁄2 + 1⌉≤ k + 3 pour obtenir
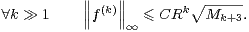 |
On notera que (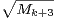 ) est une suite log-convexe. Le théorème de Denjoy-Carleman
assure alors la convergence de la série
) est une suite log-convexe. Le théorème de Denjoy-Carleman
assure alors la convergence de la série 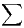
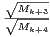 , c’est-à-dire 1) à translation d’indice
près.
, c’est-à-dire 1) à translation d’indice
près.
Lemme 2.Soit (Mk)k N une suite strictement positive et log-convexe ; au moins une deux
assertions suivantes est alors vraie :
N une suite strictement positive et log-convexe ; au moins une deux
assertions suivantes est alors vraie :
- la suite (Mk) est majorée ;
- la suite (Mk) est croissante à partir d’un certain rang,
Démonstration Si la suite (Mk) est décroissante, le point i) est immédiat. Si la suite (Mk) n’est
pas décroissante, il existe alors k0  N tel que Mk0 ≤ Mk0+1. Par log-convexité, on a
M
N tel que Mk0 ≤ Mk0+1. Par log-convexité, on a
M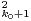 ≤ Mk0Mk0+2. Ce qui nous donne Mk0+1 ≤ Mk0+2. Une récurrence immédiate assure la
croissance de (Mk) à partir du rang k0. cqfd
≤ Mk0Mk0+2. Ce qui nous donne Mk0+1 ≤ Mk0+2. Une récurrence immédiate assure la
croissance de (Mk) à partir du rang k0. cqfd
4.Implication 5) ⇒ 4) du théorème 1
Appliquons l’assertion 5) pour la suite (Mk-1)k≥1 (on notera que la log-convexité est invariante par translation d’indice). On cherche une estimation de la forme suivante :
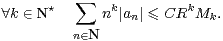 |
On applique l’inégalité de Cauchy-Schwarz et l’égalité de Parseval :
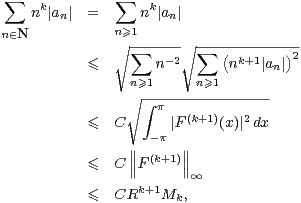
5.Implication 4) ⇒ 3) du théorème 1
Il s’agit précisément de la formule (2) de la réponse R897.
6.Implication 3) ⇒ 5) du théorème 1
Rappelons que la loi d’une variable aléatoire est déterminée par sa fonction caractéristique.
Proposition 5.Soient X et Y deux variables aléatoires. Alors se valent
- X et Y ont la même loi,
- pour tout t
 R, on a E[exp(itX)] = E[exp(itY )].
R, on a E[exp(itX)] = E[exp(itY )].
Démonstration Seul le sens ii) ⇒ i) doit être démontré. On doit prouver que pour toute fonction
ϕ 
 0 (R , C ), à support compact, on a E[ϕ(X)] = E[ϕ(Y )]. Or il existe une suite (ϕn)n
0 (R , C ), à support compact, on a E[ϕ(X)] = E[ϕ(Y )]. Or il existe une suite (ϕn)n N de
fonctions de classe
N de
fonctions de classe  ∞ sur R, à support compact, qui vérifie
∞ sur R, à support compact, qui vérifie
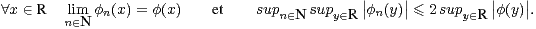 |
La démonstration de ce dernier point est laissée au lecteur (par exemple avec un argument de convolution). Le théorème de la convergence dominée montre que (E[ϕn(X)])n≥0 converge vers E[ϕ(X)] (et de même en remplaçant X par Y ). Par conséquent, on pourra conclure si l’on arrive à prouver les égalités
![⋆ [ ] [ ]
∀n ∈ N E ϕn(X ) = E ϕn(Y) .](/numeros/RMS127-4/RMS127-4352x.png) | (11) |
L’idée est alors d’invoquer la formule d’inversion de la transformée de Fourier :
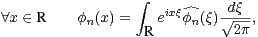 |
où l’on a noté 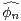 (ξ) =
(ξ) = 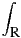 e-ixξϕ(x)
e-ixξϕ(x)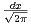 . La formule d’inversion est justifiée car la
fonction ϕn est de classe
. La formule d’inversion est justifiée car la
fonction ϕn est de classe  ∞à support compact (donc elle et sa transformée de Fourier
appartiennent à l’espace de Schwartz). Le théorème de Fubini-Lebesgue amène alors
à
∞à support compact (donc elle et sa transformée de Fourier
appartiennent à l’espace de Schwartz). Le théorème de Fubini-Lebesgue amène alors
à
![∫
E [ϕ (X )] = E[exp(iXξ)]^ϕ (ξ)√dξ-.
n R n 2π](/numeros/RMS127-4/RMS127-4357x.png) |
Cette dernière formule et ii) impliquent évidemment (11) et la preuve est finie. cqfd
On peut maintenant prouver l’implication 3) ⇒ 5) recherchée. Soient X et Y les deux variables aléatoires de l’assertion 3).
Introduisons les deux fonctions caractéristiques FX(t) = E[exp(itX)] et FY (t) = E[exp(itY )]
définies pour tout t  R. D’après la proposition 5, la fonction F := FX - FY n’est pas
identiquement nulle. Les théorèmes classiques permettent d’assurer que FX et FY sont toutes deux
de classe
R. D’après la proposition 5, la fonction F := FX - FY n’est pas
identiquement nulle. Les théorèmes classiques permettent d’assurer que FX et FY sont toutes deux
de classe  ∞ sur R et que l’on a
∞ sur R et que l’on a
![| (k) | || [k k itX k k itY]|| [ k]
∀k∈N∀t ∈ R |F (t)| = |E iX e - iY e | ≤ 2E X .](/numeros/RMS127-4/RMS127-4358x.png) |
On remarque au passage que F est plate en t = 0 et que la suite 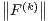 ∞ est à croissance de type
(Mk ). Il s’agit maintenant de voir que F est 2π-périodique car X et Y sont à valeurs
entières :
∞ est à croissance de type
(Mk ). Il s’agit maintenant de voir que F est 2π-périodique car X et Y sont à valeurs
entières :
![itX 2iπX itY 2iπY
F (t +2π ) = E[e e - e e ] = F(t).](/numeros/RMS127-4/RMS127-4360x.png) |
Il nous reste à vérifier que F ne fait intervenir que des fréquences positives dans son développement en série de Fourier. Mais cela est trivial car on a la somme absolument convergente :
![∑ ( )
F(t) = P [X = n]- P[Y = n]eint.
n∈N](/numeros/RMS127-4/RMS127-4361x.png) |
7.Équivalence 1) ⇔ 2) du théorème 1
On a le résultat suivant.
Proposition 6.Considérons une suite (Mk)k N strictement positive et log-convexe ; les propriétés
suivantes sont alors équivalentes :
N strictement positive et log-convexe ; les propriétés
suivantes sont alors équivalentes :
- 1)
- la série
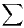
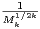 converge ;
converge ;
- 2)
- la série
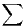
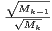 converge.
converge.
Démonstration 1) ⇒ 2). Par log-convexité, la suite de terme général 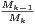 est décroissante. Cela
nous mène à
est décroissante. Cela
nous mène à
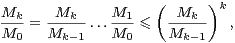 |
et l’on conclut grâce à
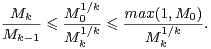 |
2) ⇒ 1). Posons ak = 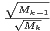 pour tout k
pour tout k  N⋆. Notons que l’on a
N⋆. Notons que l’on a
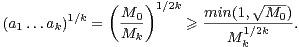 |
La conclusion découlera alors de l’inégalité de Carleman :
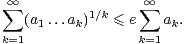 | (12) |
La preuve de l’inégalité (12) utilise l’inégalité arithmético-géométrique de la façon suivante : soit
λj = 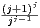 avec donc (λ1
avec donc (λ1 λk)1⁄k = k + 1. Alors
λk)1⁄k = k + 1. Alors
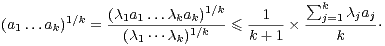 |
Ce qui nous donne par sommation, et par utilisation de l’égalité 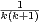 =
= 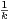 -
-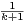 ,
,
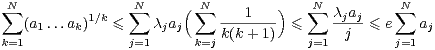
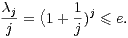
[1] Y.Katznelson, An introduction to harmonic analysis, Third edition, Cambridge University Press (2004).
[2] B.Korenbljum, Quasianalytic classes of functions in a circle, Soviet Math. Doklady, no 6 (1965), p.1155-1158.
[3] S.Mandelbrojt, Séries adhérentes, Régularisation des suites, Applications, Gauthier-Villars (1952).
[4] W.Rudin, Analyse Réelle et Complexe, chapitre 19, Troisième édition, Dunod (2009).
[5] C. Corduneanu, Almost periodic functions, 2nd edition, Chelsea Publishing Company New
York (1989).
Ω
[Table des matières]