[Table des matières]
Structure
des anneaux commutatifs
finis1 1. 2020 Mathematics Subject Classification : 11T99, 13A99, 13E10, 13H05, 13M05, 97H40
par Colas Bardavid et Éric Pité
Colas Bardavid est professeur en PCSI au Lycée Sainte-Geneviève
Résumé. On démontre, par des méthodes élémentaires, un théorème de structure pour les anneaux commutatifs finis. Ce résultat est un cas particulier d’une propriété plus générale qu’on peut décrire en termes géométriques.
Abstract. Structure of Finite Commutative Rings.
We prove, by elementary methods, a structure theorem for finite commutative rings. This result is a special case of a more general result of which we give a geometrical interpretation.
Mots-clés : anneaux commutatifs finis, anneaux locaux, idéal premier, idéal maximal, idéaux comaximaux.
Notations et conventions
Par convention, un anneau est unitaire. Tous les anneaux de ce texte seront commutatifs.
Pour faciliter la lecture, on notera avec des polices différentes les anneaux quelconques et les anneaux finis :
- les lettres A, B, etc. désigneront des anneaux commutatifs ;
- les lettres A , B, etc. désigneront des anneaux commutatifs finis.
Ce texte rassemble quelques réflexions sur les anneaux commutatifs finis. On y fait également un peu de combinatoire. On y prouve (c’est le résultat principal) un théorème de dévissage :
Théorème 1. — Pour tout anneau commutatif fini A, il existe des anneaux locaux finis A1,…,Am
tels que A est isomorphe au produit A1 × ×Am.
×Am.
- La partie 2 donne une démonstration du théorème chinois par un lemme combinatoire.
- La partie 3 présente les idéaux premiers et maximaux des anneaux commutatifs finis afin de démontrer le théorème principal dans la partie 4.
- La partie 5 présente une application du théorème principal : c’est une réponse à une question de la rubrique Questions et Réponses, qui est en fait à l’origine de cet article.
- Dans la dernière section, on montre que ce résultat de structure n’a rien de surprenant : c’est un cas particulier d’un théorème plus général portant sur les anneaux artiniens. Nous y expliquerons ce qu’est un anneau artinien et quelles interprétations géométriques on peut donner du théorème et de ces objets.
La preuve donnée n’exige aucune connaissance prérequise en algèbre commutative, si ce n’est une certaine habitude des anneaux quotients. Nous avons parsemé le texte d’exercices pour les lecteurs qui aiment les chercher.
Le théorème ci-dessus est bien connu dans le cas où A = Z⁄mZ : c’est le théorème chinois. Si
m = p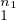
 p
p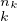 est une décomposition en produit de nombres premiers, on a un isomorphisme
d’anneaux
est une décomposition en produit de nombres premiers, on a un isomorphisme
d’anneaux
Z⁄mZ ≃Z⁄p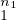 Z × Z × ×Z⁄p ×Z⁄p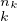 Z. Z.
|
Chaque anneau Z ⁄p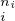 Z ne possède qu’un seul idéal maximal, il est local.
Z ne possède qu’un seul idéal maximal, il est local.
Commençons cet article par une définition. Le lecteur intéressé pourra consulter chap II §3, p. 102]Bourbaki.
Définition 1. — Un anneau commutatif A est dit local quand il possède exactement un idéal maximal1 1. En supposant l’axiome du choix (ce qu’on fera), le lemme de Zorn nous assure que tout anneau possède au moins un idéal maximal. .
Exercice 1. — Soit A un anneau commutatif.
- 1.
- Montrer que A est local si, et seulement si, A\U(A) est un idéal, où on a noté U(A) le groupe des inversibles de A.
- 2.
- Dans ce cas, caractériser l’unique idéal maximal de A.
Exercice 2. — Parmi les anneaux suivants, lesquels sont locaux ?
1. Un corps K. 2. L’anneau des entiers relatifs Z. 3. Le sous-anneau de Q dont les éléments ont des dénominateurs impairs. 4. Le sous-anneau Z(p) de Q où l’on n’autorise que les fractions dont le dénominateur est premier avec p (un nombre premier). 5. L’anneau K[[X]] des séries formelles sur le corps K. 6. L’anneau A[[X]]. 7. L’anneau des entiers p-adiques, Zp.
Exercice 3. — Soit p un nombre premier. Montrer que
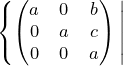 a,b,c a,b,c 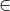 Z⁄pZ)
}
) Z⁄pZ)
}
)
|
est un anneau commutatif fini local.
On rappelle que si I et J sont des idéaux de A, le produit de I et J, noté IJ, est l’idéal de A
engendré par 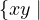 x
x  I et y
I et y  J}.
J}.
Exercice 4. — Soient A un anneau commutatif, 𝔪 un idéal maximal de A et i 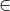 N*. En considérant le
morphisme canonique
N*. En considérant le
morphisme canonique
| A-→A⁄𝔪i |
et l’image directe par ce morphisme de l’idéal 𝔪, montrer que l’anneau quotient A⁄𝔪i est local.
2.Idéaux comaximaux et théorème chinois
Par souci de complétude, on énonce et démontre le théorème chinois. Si I et J sont des idéaux de A tels que I + J = A, on dira que I et J sont comaximaux. On trouve dans la littérature d’autres expressions pour cette propriété : ≪I et J premiers entre eux ≫ ou ≪I et J étrangers l’un à l’autre ≫ .
Exercice 5. — Pour n 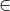 N*, on note encore n l’élément
N*, on note encore n l’élément  n fois de A.
n fois de A.
Soient A un anneau commutatif et p,q des nombres premiers distincts.
- 1.
- Montrer que (p) et (q), en tant qu’idéaux de A, sont comaximaux.
- 2.
- Soient r et s des entiers non nuls.
- (a)
- Montrer qu’il en est de même pour (pr) et (qs).
- (b)
- Montrer que 𝔪r et 𝔫s sont comaximaux, où 𝔪, 𝔫 sont des idéaux maximaux distincts de A.
Dans la suite, n est un entier naturel non nul.
Proposition 1 (Théorème chinois). — Soient I1,…,In des idéaux d’un anneau commutatif A deux à deux comaximaux.
- 1.
- La flèche produit A-→
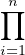 A⁄Ii des projections canoniques est surjective.
A⁄Ii des projections canoniques est surjective.
- 2.
- Ainsi, on a A⁄(I1 ∩
 ∩ In) ≃
∩ In) ≃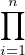 A⁄Ii.
A⁄Ii.
- 3.
- On a I1 ∩
 ∩ In = I1
∩ In = I1 In.
In.
Un lemme combinatoire
On va utiliser dans notre preuve un lemme combinatoire. Dans la suite, on note
Δn := 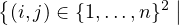 i < j}
; i < j}
;
|
cet ensemble est muni des deux projections pi : Δn -→{1,…,n} pour i = 1,2.
Pour E ⊂ Δn , on s’intéresse à l’ensemble d’indices
| I(E) := p1(E) ∪ p2(Δn \ E). |
composé des premières coordonnées des éléments de E et des secondes coordonnées des éléments de Δn \ E.
Lemme 1. — Soit E une partie de Δn. Alors,
I(E) = {1,…,n} ou ∃i0  {1,…,n}, I(E) = {1,…,n}\ {1,…,n}, I(E) = {1,…,n}\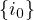 . .
|
Démonstration On suppose que I(E)≠{1,…,n}. Soit i0 un indice qui n’est pas dans I(E). Soit j > i0 ; alors (i0 , j) ne peut pas être dans E et est donc dans Δn \E. Donc p2(i0,j), qui vaut j, est dans I. Si j < i0 , on raisonne de même avec (j,i0).
Exercice 6. — De façon plus générale, si P est une partie de {1,…,n}2 et si E ⊂ P , on note
| IP(E) := p1(E) ∪ p2(P \ E). |
On dit que P évite au plus k indices si ∀E ⊂ P, card {1,…,n}\IP(E)
{1,…,n}\IP(E) ≤ k. On appelle degré
d’évitement de P et on note e(P) l’entier
≤ k. On appelle degré
d’évitement de P et on note e(P) l’entier
e(P) := maxE⊂P card {1,…,n}\IP(E) {1,…,n}\IP(E)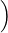 . .
|
Ainsi, le lemme signifie que le degré d’évitement de Δn vaut au plus 1.
- 1.
- Montrer que e(Δn) = 1.
- 2.
- Montrer que si P contient Δn, alors P évite au plus un indice.
- 3.
- Montrer que {1,…,n}2 n’évite aucun indice, c’est-à-dire que e({1,…,n}2) = 0.
- 4.
- Quelles sont les parties P de {1,…,n}2 telles que e(P) = 1 ?
Lemme 2. — Soient I1,…,In des idéaux d’un anneau commutatif A deux à deux comaximaux. Alors, il existe des éléments x1,…xn tels que
∀i  {1,…,n} xi {1,…,n} xi  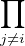 Ij et x1 + Ij et x1 +  + xn = 1. + xn = 1.
|
Démonstration Comme, les Ii sont deux à deux comaximaux, fixons, pour tout (i,j)  Δn, des
éléments a(i,j)
Δn, des
éléments a(i,j)  Ii et b(i,j)
Ii et b(i,j)  Ij tels que
Ij tels que
| a(i,j) + b(i,j) = 1. |
On a donc
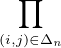 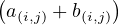 = 1. = 1.
|
On développe ce produit : pour chaque parenthèse, on choisit soit a, soit b. Formellement, cela donne :
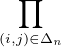 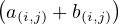 = = 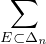 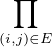 a(i,j) a(i,j) b(i,j). b(i,j).
|
Fixons E ⊂ Δn , et notons
x := 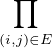 a(i,j) a(i,j)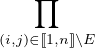 b(i,j). b(i,j).
|
Si I (E) = {1, … , n}\{i0} pour un i0, alors on a x 
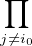 Ij. Si I(E) = {1,…,n}, on a x
Ij. Si I(E) = {1,…,n}, on a x 
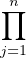 Ij,
donc en particulier x
Ij,
donc en particulier x 
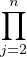 Ij, par exemple.
Ij, par exemple.
Ainsi, chaque élément dans cette somme est dans un 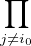 Ij pour un i0 bien choisi.
Ij pour un i0 bien choisi.
Donc, en regroupant les éléments x qui appartiennent au même produit d’idéaux, on en déduit qu’il existe x1 , … xn tels que
∀i  {1,…,n} xi {1,…,n} xi  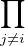 Ij et x1 + Ij et x1 +  + xn = 1. + xn = 1.
|
cqfd
Démonstration de la proposition .
Fixons-nous une telle décomposition de l’unité ; elle nous permet de prouver les trois points du théorème chinois.
- 1.
- Soit (ai )1≤i≤n une famille dans An. On pose x := a1x1 +
 + anxn.
+ anxn.
On vérifie alors que, pour tout i, x = ai (mod Ii) : le morphisme
A-→ 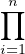 A⁄Ii
A⁄Ii
est donc bien surjectif.
- 2.
- Il suffit de remarquer que le noyau de la flèche précédente est I1 ∩
 ∩ In.
∩ In.
- 3.
- On veut montrer que I1 ∩
 ∩ In = I1
∩ In = I1 In. L’inclusion ⊃ est toujours vraie. Soit
maintenant x
In. L’inclusion ⊃ est toujours vraie. Soit
maintenant x  I1 ∩
I1 ∩ ∩ In. Alors, en multipliant x par la décomposition de l’unité, on
trouve
∩ In. Alors, en multipliant x par la décomposition de l’unité, on
trouve
x =  xxi.
xxi.
Or, pour tout i, xxi
 I1
I1 In, d’où le résultat.
In, d’où le résultat.
Étude d’un exemple
On va voir dans cet exemple que la preuve donnée ci-dessous est effective.
- On considère les nombres premiers 5, 7 et 11.
- On a les relations de Bézout
3 ⋅7 - 4 ⋅5 = 1 1 ⋅11 - 2 ⋅5 = 1 2 ⋅11 - 3 ⋅7 = 1. - En les multipliant entre elles, comme dans la preuve, on obtient la décomposition de l’unité
suivante :
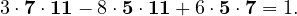
(1) - Voyons maintenant comment cette décomposition de l’unité permet de résoudre les systèmes
de congruences. Par exemple, résolvons
(S) : 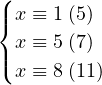 .
.
En suivant la démonstration du théorème chinois, on trouve qu’une solution de (S) est
x := 1 ⋅ 3 ⋅7 ⋅11 + 5 ⋅ (-8) ⋅5 ⋅11 + 8 ⋅ 6 ⋅5 ⋅7 = -289. Cette méthode permet, une fois qu’on a obtenu la décomposition () de l’unité, de résoudre le système (S) pour tous les restes modulo 5, 7 et 11.
3.Idéaux premiers et maximaux des anneaux finis
Proposition 2. — Les idéaux premiers d’un anneau commutatif fini A sont ses idéaux maximaux.
Démonstration En effet, si 𝔭 est un idéal premier de A, alors A ⁄𝔭 est un anneau intègre fini. Or, on sait que les anneaux intègres finis sont forcément des corps. Donc, 𝔭 est maximal. Réciproquement, un idéal maximal est toujours premier. cqfd
Rappelons que pour un anneau commutatif A, on note Nil(A) l’ensemble des éléments nilpotents de A : c’est le nilradical de A.
Exercice 7. — Montrer que Nil(A) est un idéal de A.
On note 𝔪1 , 𝔪2 , ..., 𝔪n les idéaux maximaux d’un anneau commutatif fini A.
Proposition 3. — On a l’égalité
𝔪1𝔪2 𝔪n = Nil(A). 𝔪n = Nil(A).
|
Démonstration Déjà, comme les 𝔪i sont comaximaux, on a 𝔪1𝔪2 𝔪n = ⋂
𝔪n = ⋂
 𝔪i. Soit 𝔪 l’un
des idéaux maximaux. Soit x
𝔪i. Soit 𝔪 l’un
des idéaux maximaux. Soit x  Nil(A) et soit p
Nil(A) et soit p  N* tel que xp = 0. On a xp
N* tel que xp = 0. On a xp  𝔪. Comme 𝔪 est
premier, x appartient à 𝔪.
𝔪. Comme 𝔪 est
premier, x appartient à 𝔪.
Traitons l’autre inclusion.
Soit x un élément non nilpotent de A. On considère S =  . On considère les idéaux I
de A tels que I ∩ S = ∅. Il y en a au moins un, à savoir (0). Soit I0 un tel idéal, que l’on suppose
maximal2
pour la propriété indiquée.
. On considère les idéaux I
de A tels que I ∩ S = ∅. Il y en a au moins un, à savoir (0). Soit I0 un tel idéal, que l’on suppose
maximal2
pour la propriété indiquée.
Montrons que I0 est premier. Soient a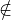 I0 et b
I0 et b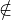 I0. Alors, par maximalité de I0, on sait que
I0 + (a) intersecte S. On peut donc écrire
I0. Alors, par maximalité de I0, on sait que
I0 + (a) intersecte S. On peut donc écrire
| αa + i0 = xp, |
où α  A, i0
A, i0  I0 et p
I0 et p  N. De même, on écrit βb + i0ʹ = xq. En multipliant ces deux relations, on
obtient γab + i0 ʹʹ = xp+q. Donc, nécessairement, ab
N. De même, on écrit βb + i0ʹ = xq. En multipliant ces deux relations, on
obtient γab + i0 ʹʹ = xp+q. Donc, nécessairement, ab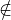 I0.
I0.
Ainsi, I0 est premier et donc maximal. La définition de I0 entraîne que x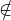 I0 et, par conséquent,
que x
I0 et, par conséquent,
que x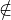 𝔪1 𝔪2
𝔪1 𝔪2  𝔪n.
𝔪n.
Par contraposition, on a ainsi 𝔪1𝔪2 𝔪n ⊂ Nil(A). cqfd
𝔪n ⊂ Nil(A). cqfd
Proposition 4. — Il existe q1, …, qn des entiers non nuls tels que
𝔪1q1
𝔪2q2
 𝔪nqn
= (0). 𝔪nqn
= (0).
|
Démonstration Comme A est fini, il existe N tel que
∀x  Nil(A), xN = 0. Nil(A), xN = 0.
|
On considère 𝔪 un idéal maximal de A ; on note p son cardinal.
Soient q  N et x1,x2,…,xq
N et x1,x2,…,xq  𝔪. Comme A est fini, si q est suffisamment grand, ≪ on sera obligé
de prendre plusieurs fois le même xi ≫. Plus précisément, d’après le principe des tiroirs, si
q ≥ p(N - 1) + 1, l’un des xi apparaît au moins N fois dans le produit x1x2
𝔪. Comme A est fini, si q est suffisamment grand, ≪ on sera obligé
de prendre plusieurs fois le même xi ≫. Plus précisément, d’après le principe des tiroirs, si
q ≥ p(N - 1) + 1, l’un des xi apparaît au moins N fois dans le produit x1x2 xq. Ainsi, il existe
q
xq. Ainsi, il existe
q  N tel que
N tel que
𝔪q ⊂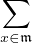 (xN). (xN).
|
On note qi un tel entier pour 𝔪i. Montrons que
𝔪1q1
𝔪2q2
 𝔪nqn
= (0). 𝔪nqn
= (0).
|
Cet idéal est engendré par les éléments du type
a := 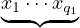  𝔪1q1 × 𝔪1q1 × × ×  𝔪nqn. 𝔪nqn.
|
D’après ce qu’on vient de dire, x1 xq1 peut s’écrire xNxʹ, avec x,xʹ
xq1 peut s’écrire xNxʹ, avec x,xʹ 𝔪1 ; et de même pour les
autres éléments. Ainsi, a peut s’écrire
𝔪1 ; et de même pour les
autres éléments. Ainsi, a peut s’écrire
a = (y1 yn)Nt, yn)Nt,
|
où yi  𝔪i et t
𝔪i et t  A. Comme on a démontré dans la proposition précédente que
A. Comme on a démontré dans la proposition précédente que
𝔪1𝔪2 𝔪n = Nil(A) ; 𝔪n = Nil(A) ;
|
on a donc a = 0. D’où le résultat. cqfd
Remarque : cas infini
La proposition est une version finie du résultat suivant.
Exercice 8. — Soit A un anneau commutatif. Montrer que l’intersection de tous les idéaux premiers de A égale le nilradical de A.
On va avoir besoin des résultats de l’exercice 4 et de l’exercice suivant :
Exercice 9. — Soient A un anneau commutatif et I un idéal de A. Les idéaux de A⁄I sont en bijection croissante avec les idéaux de A contenant I.
4.1.Théorème de dévissage des anneaux finis
On peut maintenant démontrer le résultat principal de ce texte :
Théorème 2. — Tout anneau fini commutatif s’écrit comme produit fini d’anneaux locaux.
Démonstration On choisit des entiers qi comme dans la proposition . D’après l’exercice , les 𝔪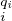 sont deux à deux comaximaux. On a donc
sont deux à deux comaximaux. On a donc
⋂
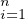 𝔪 𝔪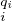 = = 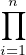 𝔪 𝔪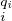 = (0). = (0).
|
Le théorème chinois nous dit donc que A≃A ⁄(0) ≃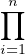 A ⁄𝔪
A ⁄𝔪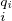 . De plus, d’après l’exercice 4, les
A ⁄𝔪
. De plus, d’après l’exercice 4, les
A ⁄𝔪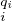 sont des anneaux locaux. cqfd
sont des anneaux locaux. cqfd
On aimerait en savoir plus sur les anneaux finis locaux. Commençons par montrer :
Proposition 5. — Soit A un anneau local fini, alors |A| est une puissance d’un nombre premier.
Lemme 3. — Un anneau local A a pour caractéristique zéro ou la puissance d’un nombre premier.
Démonstration Soit A un anneau local et 𝔪 son unique idéal maximal. Supposons que A soit de
caractéristique non nulle k = ab, avec a,b > 1 et pgcd(a,b) = 1. Alors a,b  𝔪, donc 1
𝔪, donc 1  𝔪 ce
qui est impossible. cqfd
𝔪 ce
qui est impossible. cqfd
Lemme 4. — Soient G un groupe abélien fini et p un nombre premier divisant |G|. Alors G possède un élément d’ordre p.
Démonstration Soient x1,…,xk des éléments de G qui l’engendrent.
Notons Gi le sous-groupe cyclique engendré par xi et ψ le morphisme de 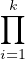 Gi dans G qui à
(t1 , … , tk ) associe le produit t1
Gi dans G qui à
(t1 , … , tk ) associe le produit t1 tk.
tk.
D’après le premier théorème d’isomorphisme, on a 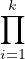 |Gi| = |G|×|Kerψ|.
|Gi| = |G|×|Kerψ|.
De plus p divise |G|, donc il divise l’un des |Gi|, ainsi une des puissances de l’un des xi est d’ordre p. cqfd
Au passage, remarquons que le lemme est encore vrai quand G n’est pas abélien ; dans ce cas, il s’appelle théorème de Cauchy.
Démonstration de la proposition . Soit A un anneau local fini ; notons pn sa caractéristique, où p est
un nombre premier et où n  N*.
N*.
Supposons que |A| ne soit pas une puissance de p et considérons q un nombre premier
divisant |A| tel que q≠p. On considère maintenant le groupe fini (A,+). D’après le lemme ,
on sait qu’il existe x  A dont l’ordre (additif) vaut q. On a donc qx = 0 ; on a aussi
pn x = 0. Avec une relation de Bézout, on a donc x = 0 ; c’est absurde car l’ordre de x vaut
q≠ 1.
A dont l’ordre (additif) vaut q. On a donc qx = 0 ; on a aussi
pn x = 0. Avec une relation de Bézout, on a donc x = 0 ; c’est absurde car l’ordre de x vaut
q≠ 1.
Ainsi, |A| est une puissance de p. cqfd
La proposition nous donne une condition nécessaire pour qu’un anneau fini soit local, mais cette
condition n’est pas suffisante. En effet, l’anneau 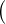 Z⁄pZ
Z⁄pZ 2 n’est pas local ; cela découle de la
première question de l’exercice suivant.
2 n’est pas local ; cela découle de la
première question de l’exercice suivant.
Exercice 10. — Soient A1, …, An des anneaux commutatifs. On considère B = A1 × ×An.
×An.
- 1.
- Montrer que les idéaux maximaux de B sont tous du type
A1 ×  ×Ai-1 ×𝔪i ×Ai+1 ×
×Ai-1 ×𝔪i ×Ai+1 × ×An,
×An,
où 𝔪i est un idéal maximal de Ai.
- 2.
- Décrire les idéaux premiers de B.
Ainsi, compter le nombre d’éléments ne suffit pas. En revanche si l’on compte le nombre d’éléments de l’anneau et le nombre de diviseurs de zéro, on peut dire si un anneau fini est local.
Théorème 3. — Un anneau commutatif fini A est local si, et seulement si, il existe un nombre premier p et deux entiers m,n avec m < n, tels que |A| = pn et A a pm diviseurs de zéro.
On peut trouver des preuves dans Theorem 3]Behboodi ou Theorem 2]Gonzalez.
5.Application aux groupes des éléments inversibles d’un anneau fini
Le point de départ de cet article était pour les auteurs la résolution de la question Q556 d’Hervé Pépin :
Question.Soit n un entier pair. Existe-t-il un anneau commutatif fini A dont le groupe U(A) des éléments inversibles possède exactement n éléments ?
Dans la RMS 128-4, Philippe Bonnet fournit une caractérisation complète des cardinaux de U(A) possibles. Notre approche, qui repose sur le dévissage des anneaux finis, est plus élémentaire — mais moins complète — que celle de Philippe Bonnet.
Proposition 6. — Il n’existe pas d’anneau commutatif fini A dont le groupe U(A) des éléments inversibles possède exactement 34 éléments. De plus, 34 est le plus petit entier pair ayant cette propriété.
Démonstration On procède en deux parties :
∙ L’entier 34 convient.
Supposons qu’il existe un anneau commutatif fini A dont le groupe des inversibles U(A) possède exactement 34 éléments.
Appliquons le théorème à A : on écrit A≃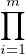 Ai, où les Ai sont des anneaux locaux, et on note 𝔪i
leurs uniques idéaux maximaux. On a |U(A)| =
Ai, où les Ai sont des anneaux locaux, et on note 𝔪i
leurs uniques idéaux maximaux. On a |U(A)| = 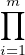 |U(Ai)|.
|U(Ai)|.
Il existe donc au plus deux Ai tels que |U(Ai)| > 1. On distingue deux cas.
- 1.
- Il y a deux anneaux Ai tels que |U(Ai)| > 1.
Dans ce cas, alors, pour l’un d’entre eux on a |U(Ai)| = 17.
On a Ai = 𝔪i ⊔ U(Ai) donc |Ai| = |𝔪i| + |U(Ai)|. Comme |𝔪i| divise |Ai|, il divise aussi |U(Ai )|. Donc, |𝔪i| {1,17}.
{1,17}.
Examinons ces deux cas.- Si |𝔪i | = 1, alors 𝔪 est réduit à {0} et Ai est un corps. De plus |Ai| = 18, ce qui est impossible car 18 n’est pas une puissance entière d’un nombre premier.
- Si |𝔪i | = 17, alors |Ai| = 34 ce qui contredit la proposition .
- 2.
- Il y a un seul anneau Ai tel que |U(Ai)| > 1.
Fixons cet anneau Ai. On a |U(Ai)| = 34.
Comme précédemment, on a |Ai| = |𝔪i| + |U(Ai)| et l’entier |𝔪i| divise |U(Ai)|.
Donc |𝔪i | {1,2,17,34}. Examinons chacun de ces cas.
{1,2,17,34}. Examinons chacun de ces cas.
- Si |𝔪i | = 1, alors 𝔪i est réduit à {0} et Ai est un corps. De plus |Ai| = 35, ce qui est impossible car 35 n’est pas une puissance entière d’un nombre premier.
- Si |𝔪i| = 2, alors le corps Ai⁄𝔪i possède 18 éléments, ce qui est aussi impossible.
- Si |𝔪i | = 17 (resp. 34), alors |Ai| = 51 (resp. 68), ce qui contredit la proposition .
Ainsi, un anneau fini A ne peut pas être tel que |U(A)| = 34.
∙ L’entier 34 est le plus petit entier pair qui convient.
Notons φ la fonction indicatrice d’Euler, et si p est un nombre premier, Fpr ≪ le ≫ corps à pr éléments.
Soit n un entier pair tel que l’équation φ(x) = n d’inconnue x admette au moins une solution, qu’on note m. Dans ce cas, l’anneau Z⁄mZ est tel que son groupe des inversibles possède exactement n éléments.
On dit qu’un entier naturel n est un anti-indicateur si l’équation φ(x) = n d’inconnue x n’admet pas de solution. Les premiers anti-indicateurs pairs sont : 14, 26, 34.
Pour trouver un entier pair n, tel qu’il n’existe aucun anneau commutatif fini A dont le groupe des inversibles U(A) possède exactement n éléments, il faut nous tourner vers les anti-indicateurs.
L’entier n = 14 ne convient pas car 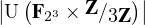 = 14.
= 14.
L’entier n = 26 ne convient pas non plus car |U(F33)| = 26. cqfd
6.Anneaux artiniens, noethériens et géométrie algébrique
6.1.Anneaux artiniens, noethériens
Le théorème est un cas particulier d’un théorème plus général.
Définition 2. — Un anneau commutatif A est dit artinien3 quand toute suite décroissante d’idéaux est stationnaire ; il est dit noethérien4 quand toute suite croissante d’idéaux est stationnaire.
Exercice 11. — Montrer que A est artinien (resp. noethérien) si, et seulement si, toute partie non vide d’idéaux de A admet un élément minimal (resp. maximal) pour la relation d’inclusion.
Théorème 4. — Un anneau artinien est un produit fini d’anneaux locaux artiniens.
Ce théorème peut se montrer en utilisant des techniques de localisation. On pourra par exemple consulter Théorème 26 page 75]Goblot.
Parmi les résultats intermédiaires qu’on a montrés dans le cas des anneaux finis, un certain nombre est encore vrai pour les anneaux artiniens :
- les idéaux premiers et maximaux y coïncident ;
- un anneau artinien n’a qu’un nombre fini d’idéaux maximaux : 𝔪1,…,𝔪n ;
- il existe q1 ,…,qn des entiers non nuls tels que 𝔪1q1
 𝔪nqn = (0).
𝔪nqn = (0).
6.2.Exemples d’anneaux locaux artiniens
- Tout corps k est un anneau local artinien.
- Si p est un nombre premier et n
 N*, Z⁄pnZ est un anneau local artinien, d’idéal
maximal (p).
N*, Z⁄pnZ est un anneau local artinien, d’idéal
maximal (p).
- Plus généralement, tout anneau fini local est artinien.
- Si k est un corps et n
 N*, alors k[X]⁄(Xn) est un anneau local artinien, d’idéal
maximal (X).
N*, alors k[X]⁄(Xn) est un anneau local artinien, d’idéal
maximal (X).
Exercice 12. — Soient p un nombre premier et n,m 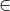 N, n ≥ 2. L’anneau
N, n ≥ 2. L’anneau
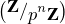 [X]⁄(Xm) [X]⁄(Xm)
|
est-il artinien ? Local ? Si oui, quel est son idéal maximal ?
6.3.Géométrie algébrique (théorie des schémas)
La théorie des schémas (, développée par Alexandre Grothendieck et ses collaborateurs à partir de la fin des années 1950) permet de voir les anneaux comme des ≪ espaces géométriques ≫ : si A est un anneau commutatif, on lui associe son spectre, noté SpecA, qui est un ≪espace ≫ 5 , appelé schéma affine. La catégorie des anneaux commutatifs est équivalente à la catégorie des schémas affines. Ce dictionnaire anneaux–espaces fonctionne à merveille. Les anneaux locaux artiniens apparaissent, dans ce dictionnaire, comme les analogues algébriques des points6 . Références
[1] Behboodi M., Beyranvand R., On the Structure of Commutative Rings with
p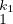
 p
p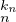 , (1 ≤ ki ≤ 7) Zero-Divisors, European Journal of Pure and Applied
Mathematics, Vol. 3, No. 2, 2010, 303-316.
, (1 ≤ ki ≤ 7) Zero-Divisors, European Journal of Pure and Applied
Mathematics, Vol. 3, No. 2, 2010, 303-316.
[2] Bourbaki N., Éléments de Mathématique, Algèbre commutative Chapitres 1 à 4. Masson, 1985.
[3] Goblot R., Algèbre commutative. Cours et exercices résolus, Masson 1996, ISBN 2-225-85308-8.
[4] González M. J., On Distinguishing Local Finite Rings from Finite Rings Only by Counting Elements and Zero Divisors, European Journal of Pure and Applied Mathematics, Vol. 7, No. 1, 2014, 109-113.
[5] Grothendieck, A., Éléments de géométrie algébrique. I. Le langage des schémas. Inst. Hautes Études Sci. Publ. Math., (4):228, 1960.
[Table des matières]


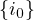 .
.